Cho tam giác ABC vuông cân tại A, AB = 4cm. Gọi M, N, I lần lượt là trung điểm của các đoạn thẳng BC, AC và BN. Điểm D thuộc đoạn thẳng AM sao cho AM = 4AD. Chứng minh tam giác DIN vuông cân
doanhnhannguyenthinh@gmail.com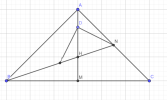
[imath]AC=4\sqrt2\Rightarrow AM=2\sqrt2[/imath]
[imath]\Rightarrow AD=\dfrac{AM}4=\dfrac{\sqrt2}{2}; AH=\dfrac{2AM}3=\dfrac{4\sqrt2}{3}[/imath]
[imath]\Rightarrow DH=AH-AD=\dfrac{5\sqrt2}6[/imath]
[imath]AN=2; DN^2=AD^2+AN^2-2AD.AN\cos 45^\circ\Rightarrow DN=\dfrac{\sqrt{10}}{2}[/imath]
[imath]BN=\sqrt{AB^2+AN^2}=2\sqrt5[/imath]
[imath]\Rightarrow HN=\dfrac{2\sqrt5}3[/imath]
[imath]\cos HND=\dfrac{DN^2+HN^2-DH^2}{2DN.NH}=\dfrac{sqrt2}2\Rightarrow \widehat{HND}=45^\circ[/imath]
[imath]IN=\dfrac{BN}2=\sqrt5[/imath]
[imath]ID=DN^2+IN^2-2DN.IN\cos \widehat{HND}=\dfrac{\sqrt{10}}2[/imath]
Xét [imath]\Delta IDN[/imath] có [imath]ID=DN; \widehat{HND}=45^\circ\Rightarrow DIN[/imath] vuông cân tại D
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em xem thêm tại
Ôn tập toán các dạng bài hình học 9
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


