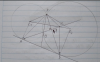
Vẽ đường thẳng vuông góc với AP qua B cắt đường thẳng qua A vuông góc với BP tại D. Gọi Q là giao điểm thứ 2 của [TEX](O_1),(O_2)[/TEX], I là giao điểm của PQ với AB. Gọi C là giao điểm của đường thẳng qua P vuông với AP và AD, E là giao điểm của đường thẳng qua P vuông góc với BP và BD.
Ta sẽ chứng minh bài toán tương đương, đó là EC trùng với [TEX]O_1O_2[/TEX].
Dễ thấy I là trung điểm của AB, P là trực tâm tam giác ADB.
Lại có: [TEX]\widehat{AQP}=\widehat{PAB}=\widehat{PDB},\widehat{BQP}=\widehat{ABP}=\widehat{ADP} \Rightarrow \widehat{AQB}=\widehat{ADB}[/TEX]
Từ đó ADQB nội tiếp. Mặt khác, kéo dài PI cắt [TEX](ADQB)[/TEX] tại M thì APBM là hình bình hành.
Khi đó ta thấy [TEX]DA \perp AM[/TEX] nên DM là đường kính của [TEX](ADQB) \Rightarrow \widehat{DQP}=\widehat{DQM}=90^o \Rightarrow PQ \perp AQ[/TEX].
Bây giờ ta sẽ chứng minh P, Q đối xứng nhau qua EC. Vẽ [TEX]PK \perp CE[/TEX] tại K cắt AB tại I'.
Qua A và B vẽ các đường thẳng song song với CE cắt PI' tại R,S.
Dễ thấy [TEX]\Delta PKC \sim \Delta ARP \Rightarrow \frac{AR}{KP}=\frac{PA}{PC}[/TEX]
[TEX]\Delta PKE \sim \Delta BSP \Rightarrow \frac{BS}{PK}=\frac{PB}{PE}[/TEX]
[TEX]\Delta PCA \sim \Delta PEB \Rightarrow \frac{PA}{PC}=\frac{PB}{PE} \Rightarrow \frac{AR}{KP}=\frac{BS}{PK} \Rightarrow AR=BS[/TEX]
Theo định lí Thales thì [TEX]I'[/TEX] là trung điểm AB hay [TEX]PI \perp EC \Rightarrow PQ \perp EC[/TEX]
Xét tam giác PQD thì CE đi qua trung điểm của DP(do DCPE là hình bình hành) và [TEX]CE \parallel DQ[/TEX] nên CE đi qua trung điểm PQ. Mà [TEX]CE \perp PQ[/TEX] nên P, Q đối xứng nhau qua CE. Từ đó ta có đpcm.
Nếu bạn có thắc mắc gì có thể hỏi tại topic này nhé. Chúng mình luôn sẵn sàng hỗ trợ bạn.
Bạn cũng có thể tham khảo một số bài toán khác tại đây.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
