Vật lí Chứng minh mặt có điện thế bằng 0 là mặt cầu

[thangsv01@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

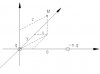
Hai điện tích điểm q và -nq (n>1) đặt tại A,B cách nhau đoạn a. Chứng minh rằng mặt có điện thế bằng 0 là mặt cầu. Tính bán kính R của mặt cầu và vị trí tâm O của mặt cầu. Áp dụng với n = 2, a = 6cm.

 

[Tùy Phong Khởi Vũ]

Chọn hệ trục tọa độ gắn với q như hình.

Xét 1 điểm M (x, y, z) trong không gian có điện thế bằng 0.

Khi đó [TEX]U_{AM} = K\frac{q}{r} = K\frac{q}{\sqrt{x^2+y^2+z^2}}[/TEX]

[TEX]U_{BM} = K\frac{-nq}{r'} = K\frac{-nq}{\sqrt{(a - x)^2+y^2+z^2}}[/TEX]

Ta phải có [TEX]U_{AM}+U_{BM} = 0[/TEX]

Do đó được [TEX]n^2(x^2+y^2+z^2) = a^2 - 2ax + x^2 + y^2 + z^2[/TEX]

Hay [TEX](n^2 - 1)(x^2+ y^2+z^2) + 2ax - a^2 = 0[/TEX]

[TEX]x^2+ y^2+z^2 + \frac{2a}{n^2 - 1}.x - \frac{a^2}{n^2 - 1} = 0[/TEX]

Đây là pt mặt cầu với tâm là [TEX]I(\frac{a}{n^2-1};0;0)[/TEX]

và bán kính là [TEX]R = \sqrt{(\frac{a}{n^2-1})^2 +\frac{a^2}{n^2 - 1}} [/TEX]