- 3 Tháng một 2018
- 311
- 257
- 86
- 21
- Nam Định
- Trường THCS Yên Trung
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
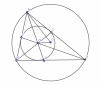
Cho tam giác ABC (AB < AC) ngoại tiếp ( O,R) . Gọi D,E,F lần lượt là giao điểm của AO với BC , BO với AC , CO với AB. (O';R') là tâm đường tròn ngoại tiếp tam giác ABC. CMR:
$ \frac{1}{AD} + \frac{1}{BE} + \frac{1}{CF} < \frac{2}{R' - OO'} $
Help mee...
$ \frac{1}{AD} + \frac{1}{BE} + \frac{1}{CF} < \frac{2}{R' - OO'} $
Help mee...