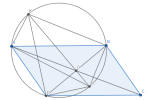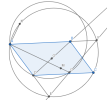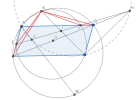
Gọi [imath]I,H[/imath] lần lượt là giao điểm của [imath]CK,DB[/imath] với [imath]EF[/imath]. Ta sẽ chứng minh [imath](EF,IH)=-1[/imath].
Thật vậy, ta dễ thấy [imath]K[/imath] là điểm chính giữa cung nhỏ [imath]EF[/imath] nên [imath]CK[/imath] là phân giác của [imath]\widehat{ECF}[/imath]
Từ đó [imath]\dfrac{IE}{IF}=\dfrac{CE}{CF}[/imath]
Áp dụng định lý Menelaus cho [imath]\Delta AEF[/imath] có [imath]M,D,B[/imath] thẳng hàng ta được [imath]\dfrac{ME}{MF} \cdot \dfrac{BF}{BA} \cdot \dfrac{DA}{DE}=1[/imath]
[imath]\Rightarrow \dfrac{ME}{MF}=\dfrac{AB \cdot DE}{AD \cdot BF}[/imath]
Từ đó ta chứng minh [imath]\dfrac{CE}{CF}=\dfrac{AB \cdot DE}{AD \cdot BF}[/imath] là được.
[imath]\Leftrightarrow \dfrac{\sin \widehat{CFE}}{\sin \widehat{CEF}}=\dfrac{AB}{BC} \cdot \dfrac{DE}{BF}[/imath]
[imath]\Leftrightarrow \dfrac{\sin \widehat{CFE}}{\sin \widehat{CEF}}=\dfrac{\sin \widehat{ACB}}{\sin \widehat{BAC}} \cdot \dfrac{DE}{BF}[/imath]
Mà [imath]\widehat{CFE}=\widehat{CAE}=\widehat{ACB}, \widehat{CEF}=\widehat{CAB}[/imath] nên ta chỉ cần chứng minh [imath]DE=BF[/imath].
Ta có [imath]AK[/imath] là phân giác ngoài của [imath]\widehat{BAD}[/imath] và [imath]K[/imath] thuộc trung trực của [imath]BD[/imath] nên [imath]K[/imath] chính là điểm chính giữa cung nhỏ [imath]BD[/imath] của [imath](ABD)[/imath].
Hay [imath]ADBK[/imath] nội tiếp [imath]\Rightarrow \widehat{DKB}=\widehat{DAB}=\widehat{EAF}=\widehat{EKF}[/imath]
[imath]\Rightarrow \widehat{EKD}=\widehat{FKB}[/imath]
Kết hợp với [imath]EK=KF[/imath] và [imath]KD=KB[/imath] ta được [imath]\Delta KED=\Delta KFB \Rightarrow ED=FB[/imath].
Vậy ta chứng minh xong nhận xét trên.
Từ [imath](EF,IH)=-1[/imath] và [imath]CI[/imath] là phân giác [imath]\widehat{ECF}[/imath] thì ta có [imath]CI \perp CH[/imath]
[imath]\Rightarrow \widehat{IHC}=90^o-\widehat{CIF}=90^o-(\widehat{IKF}+\widehat{KFE})=90^o-(\widehat{CAF}+\widehat{KAF})=90^o-\widehat{CAK}=\widehat{GAC}[/imath]
[imath]\Rightarrow AGCH[/imath] nội tiếp hay [imath]H \in (ACG)[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Chuyên đề HSGQG] Định lý LTE, cấp của số nguyên và phương trình nghiệm nguyên chứa lũy thừa
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
