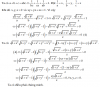[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho các số thực dương [TEX]a,b,c[/TEX] thỏa mãn [TEX]a+b+c=abc[/TEX]. Chứng minh rằng:
Em thử đặt [tex]\frac{1}{a}=x,\frac{1}{b}=y,\frac{1}{c}=z[/tex] để thu được [TEX]xy+yz+zx=1[/TEX] và biến đổi BĐT cần CM thành [tex]\sqrt{1+x^2}+\sqrt{1+y^2}-\frac{\sqrt{1+z^2}}{z}<1[/tex]. Sau đó em thử dùng HĐT [TEX]x^2+1=(x+y)(x+z)[/TEX] nhưng vẫn chưa ra ạ. Mong mọi người giúp em với ạ!!!
[tex]\frac{\sqrt{1+a^2}}{a}+\frac{\sqrt{1+b^2}}{b}-\sqrt{1+c^2}<1[/tex].
Em thử đặt [tex]\frac{1}{a}=x,\frac{1}{b}=y,\frac{1}{c}=z[/tex] để thu được [TEX]xy+yz+zx=1[/TEX] và biến đổi BĐT cần CM thành [tex]\sqrt{1+x^2}+\sqrt{1+y^2}-\frac{\sqrt{1+z^2}}{z}<1[/tex]. Sau đó em thử dùng HĐT [TEX]x^2+1=(x+y)(x+z)[/TEX] nhưng vẫn chưa ra ạ. Mong mọi người giúp em với ạ!!!