cho x,y,z>0 và x+y+z=1
cm:x+2y+z
4(1-x)(1-y)(1-z)
x+2y+z≥4(1−x)(1−y)(1−z)⇔x+y+y+z≥4(y+z)(z+x)(x+y)
Đặt
x+y=a;y+z=b;z+x=c. BĐT cần cm tương đương vs
a+b≥4abc⇔2−c−4abc≥0
Áp dụng BĐT
4ab≤(a+b)2 ta có:
2−c−4abc≥2−c−c(a+b)2=2−c−c(2−c)2=(2−c)(1−2x+c2)=(2−c)(c−1)2≥0 (do
c<a+b+c=2) (đpcm)
Dấu '=' xảy ra khi
a=b;c=1⇔x=z=21;y=0
..........................
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
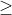 4(1-x)(1-y)(1-z)
4(1-x)(1-y)(1-z)


