a)
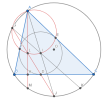
Gọi [imath]J,K[/imath] là các giao điểm khác [imath]A[/imath] của [imath]AI[/imath] và [imath]AO[/imath] với [imath](O)[/imath], [imath]L[/imath] là giao điểm của [imath]GD[/imath] và [imath]AH[/imath].
Khi đó vì [imath]\widehat{AGI}=90^o=\widehat{AGK}[/imath] nên [imath]G,I,K[/imath] thẳng hàng.
Mặt khác, ta chứng minh được [imath]\Delta GFB \sim \Delta GEC[/imath] nên [imath]\dfrac{GB}{GC}=\dfrac{BF}{CE}=\dfrac{BD}{CD}[/imath]
Suy ra [imath]GD[/imath] là phân giác của [imath]\widehat{BGC}[/imath] nên [imath]G,D,J[/imath] thẳng hàng.
Ta dễ thấy [imath]AH[/imath] và [imath]AK[/imath] đẳng giác trong [imath]\widehat{BAC}[/imath] nên [imath]\widehat{HAJ}=\widehat{JAK}[/imath]
[imath]\Rightarrow \widehat{LAI}=\widehat{LGI} \Rightarrow AGLI[/imath] nội tiếp
[imath]\Rightarrow L \in (AI)[/imath]
b)
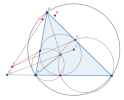
Gọi [imath]P'[/imath] là điểm liên hợp đẳng giác của [imath]P[/imath] với [imath]\Delta AEF[/imath], [imath]D'[/imath] đối xứng với [imath]P'[/imath] qua [imath]AI[/imath].
Khi đó ta thấy [imath]D' \in AP[/imath].
Lại có: [imath]\widehat{D'FE}=\widehat{K'EF}=\widehat{KEA}=\widehat{EDC}=\widehat{EFD}[/imath]. Tương tự thì [imath]\widehat{D'EF}=\widehat{DEF}[/imath] nên [imath]D'[/imath] đối xứng [imath]D[/imath] qua [imath]EF[/imath].
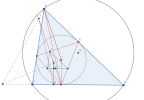
Bây giờ ta chỉ cần chứng minh [imath]AD',OI,BC[/imath] đồng quy.
Nhận thấy phép nghịch đảo tâm [imath]I[/imath] phương tích [imath]ID^2[/imath] biến đường tròn Euler của [imath]\Delta DEF[/imath] thành [imath](O)[/imath] nên [imath]IO[/imath] chính là đường thẳng Euler của [imath]\Delta DEF[/imath]. Từ đó với [imath]H[/imath] là trực tâm [imath]\Delta DEF[/imath] ta sẽ chứng minh [imath]AD',IH,BC[/imath] đồng quy.
Gọi [imath]H[/imath] là trực tâm [imath]\Delta DEF[/imath], [imath]A',B',C'[/imath] lần lượt là chân các đường cao hạ từ [imath]D,E,F[/imath] xuống [imath]BC,CA,AB[/imath]; [imath]DH[/imath] cắt [imath]B'C'[/imath] tại [imath]A_1[/imath]. Vẽ [imath]HX \perp BC[/imath] tại [imath]X[/imath] cắt [imath]B'C'[/imath] tại [imath]X'[/imath].
Dễ thấy [imath]B'C' \perp ID[/imath] nên [imath]B'C' \parallel BC[/imath]. Tương tự thì [imath]A'B' \parallel AB[/imath] và [imath]A'C' \parallel AC[/imath] nên tồn tại phép vị tự [imath]\mathcal{V}[/imath] tâm [imath]M[/imath] biến [imath]\Delta ABC[/imath] và [imath]\Delta A'B'C'[/imath].
Ta thấy [imath]H[/imath] là tâm nội tiếp của [imath]\Delta A'B'C'[/imath] nên [imath]\mathcal{V}: I \to H' \Rightarrow \mathcal{V}: X' \to D[/imath]
Từ đó [imath]A'X' \parallel AD[/imath].
Mặt khác, ta thấy [imath](DH,A_1A)=-1 \Rightarrow \dfrac{HX'}{X'X}=\dfrac{HA_1}{A_1D}=\dfrac{HA'}{A'D}=\dfrac{HA'}{A'D'} \Rightarrow D'X \parallel A'X' \parallel AD[/imath]
Kết hợp với [imath]HX \parallel ID, HD' \parallel AI[/imath] ta thấy [imath]\Delta ADI[/imath] là ảnh của [imath]\Delta D'HX[/imath] qua phép vị tự tâm [imath]N[/imath]. Khi đó [imath]AD',IH,DX[/imath] đồng quy hay [imath]AD',IH,BC[/imath] đồng quy.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Chuyên đề HSGQG] Định lý LTE, cấp của số nguyên và phương trình nghiệm nguyên chứa lũy thừa [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.




