[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
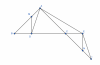
Cho $\triangle ABC$ cân tại $A$ và $\widehat{BAC} > 90^\circ$. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. lấy điểm I sao cho C là trung điểm của AI. Từ D và E kẻ các đường thẳng vuông góc với BC chúng cắt AB, AI lần lượt tại M và N
1. Chứng minh: AD = EI và $\dfrac{AD + AE}{2} > AB$
2. Chứng minh: AM + AN = AB + AC
3. chứng minh: Chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN
em cần một lời giải chi tiết, em cảm ơn ạ!
1. Chứng minh: AD = EI và $\dfrac{AD + AE}{2} > AB$
2. Chứng minh: AM + AN = AB + AC
3. chứng minh: Chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN
em cần một lời giải chi tiết, em cảm ơn ạ!
Attachments
Last edited by a moderator: