 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho tam giác đều H có cạnh bằng 8 . Chia tam giác này đều thành 64 tam giác đều có cạnh bằng 1 bởi các đường thẳng song song với các cạnh của tam giác đều đã cho. Gọi S là tập hợp các đỉnh của 64 tam giác đều có cạnh bằng 1 . Chọn Ngẫu nhiên 4 đỉnh của tập S . Tính xác suất để 4 đỉnh chọn được là bốn đỉnh của một hình bình hành nằm trong miền trong tam giác đều H . ( Mong mọi người trả lời bài viết này ạ. Cảm ơn mọi người nhiều )
A. 2/473 . B. 6/935 . C. 2/1419 . D. 2/935 .
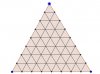
A. 2/473 . B. 6/935 . C. 2/1419 . D. 2/935 .

Last edited by a moderator:



