[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
AI GIÚP EM CÁI NÀY CÁI NÀY VỚI,EM ĐANG CẦN GẤP.CẢM ƠN Ạ
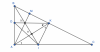
Cho tam giác $ABC$ vuông tại $A \,\,\ (AB<AC)$. Trên cạnh $BC$ lấy điểm $K$ sao cho $AB=BK$. Gọi $H$ là trung điểm $AK$. Kéo dài $BH$ cắt $AC$ tại $I$
a) Chứng minh $\triangle ABH=\triangle KBH$
b)Chứng minh $AK$ vuông góc với $BI$
c) Qua $K$ kẻ đường thẳng song song với $AC$ cắt $BH,AB$ lần lượt tại $N$ và $D$. Chứng minh $KA$ là tia phân giác của góc $IKD$
d)Kẻ $AM$ vuông góc với $BC$ tại $M$. Chứng minh 3 điểm $A,N,M$ thẳng hàng
Cho tam giác $ABC$ vuông tại $A \,\,\ (AB<AC)$. Trên cạnh $BC$ lấy điểm $K$ sao cho $AB=BK$. Gọi $H$ là trung điểm $AK$. Kéo dài $BH$ cắt $AC$ tại $I$
a) Chứng minh $\triangle ABH=\triangle KBH$
b)Chứng minh $AK$ vuông góc với $BI$
c) Qua $K$ kẻ đường thẳng song song với $AC$ cắt $BH,AB$ lần lượt tại $N$ và $D$. Chứng minh $KA$ là tia phân giác của góc $IKD$
d)Kẻ $AM$ vuông góc với $BC$ tại $M$. Chứng minh 3 điểm $A,N,M$ thẳng hàng
Attachments
Last edited by a moderator: