Cho tam giác ABC vuông cân tại A. Trên cạnh AB, AC lần lượt lấy các điểm M, N sao cho góc ABN = góc ACM = 15 độ. Gọi I là giao điểm của MC và NB. Gọi H,E,D lần lượt là trung điểm của BC,BN,CM.
a) So sánh tam giác ABN và tam giác ACM.
b) C/m tam giác ADE đều.
c) C/m 3 điểm A,I,H thẳng hàng.
d) Tính góc DHE
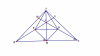
a/Xét [tex]\Delta ABN ;\Delta ACN[/tex] có
[tex]\left\{\begin{matrix} \widehat{BAC}.chung\\ AB=AC(\Delta ABC .can)\\ \widehat{ABN}=\widehat{ACM}(=15^{\circ}) \end{matrix}\right.[/tex]
[tex]\Rightarrow \Delta ABN =\Delta ACN(g.c.g)[/tex]
b/
Xét [tex]\Delta AMC[/tex] vuông tại A có AD là trung tuyến
[tex]\Rightarrow AD=DC=\frac{1}{2}MC[/tex]
cmtt : [tex]\Rightarrow AE=BE=\frac{1}{2}EN[/tex]
Mà MC=EN(theo a)
[tex]\Rightarrow \left\{\begin{matrix} AE=AD\\ \widehat{AEB}=\widehat{DAC}=15^{\circ}(do.\Delta.can ) \end{matrix}\right.[/tex]
[tex]\Rightarrow \left\{\begin{matrix} AE=AD\\ \widehat{EAD}=60^{\circ} \end{matrix}\right.[/tex]
[tex]\Rightarrow \Delta AED[/tex] đều
c/
Theo a [tex]\Rightarrow AI.pg.\widehat{EAD}[/tex]
mà [tex] \Delta AED[/tex] đều
[tex]\Rightarrow AI\perp ED[/tex]
Mà [tex]AH\perp BC(\Delta ABC.can)[/tex]
và [tex]ED//BC[/tex]
[tex]\Rightarrow A,I,H[/tex] thảng hàng
d/
Có EH là đường trung bình [tex]\Delta BNC[/tex]
[tex]\Rightarrow EH//NC\Rightarrow \widehat{EHB}=\widehat{ACB}=45^{\circ}[/tex]
CMTT:[tex]\Rightarrow \widehat{DHC}=\widehat{ABC}=45^{\circ}[/tex]
[tex]\Rightarrow \widehat{EHD}=90^{\circ}[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
