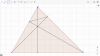
(Bấm vào hình để xem rõ hơn).
a) Ta có: [tex]\frac{AI}{HI}=\frac{S_{AIC}}{S_{HIC}}=\frac{S_{AIB}}{S_{HIB}}.[/tex]
Áp dụng tính chất dãy tỉ số bằng nhau: [tex]\frac{S_{AIC}}{S_{HIC}}=\frac{S_{AIB}}{S_{HIB}}=\frac{S_{AIC}+S_{AIB}}{S_{HIC}+S_{HIB}}[/tex]=[tex]\frac{S_{ABC}}{S_{BHC}}[/tex]
Tương tự thì ta có:[tex]\frac{BK}{HK}=\frac{S_{ABC}}{S_{AHC}}; \frac{CS}{HS}=\frac{S_{ABC}}{S_{AHB}}[/tex].
Do đó: [tex]\frac{AI}{HI}+\frac{BK}{HK}+\frac{CS}{HS}=\frac{S_{ABC}}{S_{BHC}}+\frac{S_{ABC}}{S_{AHC}}+\frac{S_{ABC}}{S_{AHB}}=[/tex][tex]S_{ABC}.(\frac{1}{S_{BHC}}+\frac{1}{S_{AHC}}+\frac{1}{S_{AHB}}).[/tex]
Giờ thì áp dụng [tex]\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{9}{a+b+c}[/tex]. Nếu anh cần thì em sẽ chứng minh bất đẳng thức này ạ.
Áp dụng cho: [tex]\frac{1}{S_{BHC}}+\frac{1}{S_{AHC}}+\frac{1}{S_{AHB}}[/tex][tex]\geq[/tex] [tex]\frac{9}{S_{BHC}+S_{AHC}+S_{AHB}}=\frac{9}{S_{ABC}}[/tex].
[tex]\Rightarrow[/tex] [tex]S_{ABC}.(\frac{1}{S_{BHC}}+\frac{1}{S_{AHC}}+\frac{1}{S_{AHB}})[/tex][tex]\geq[/tex] [tex]S_{ABC}.\frac{9}{S_{ABC}}=9[/tex]
hay [tex]\frac{AI}{HI}+\frac{BK}{HK}+\frac{CS}{HS}\geq 9[/tex](đpcm).
Theo em nghĩ câu b chỗ đó phải là [tex]cos^{2}A[/tex] đúng không ạ.
b) Ta có thể dễ dàng chứng minh được [tex]\Delta ABK\sim \Delta ACS(g-g)\Rightarrow \frac{AS}{AK}=\frac{AC}{AB}\Rightarrow \frac{AS}{AC}=\frac{AK}{AB}.[/tex](1)
Từ (1) thì ta lại chứng minh được: [tex]\Delta ASK\sim \Delta ACB(c-g-c)[/tex].
[tex]\Rightarrow \frac{S_{ASK}}{S_{ABC}}=(\frac{AS}{AC})^2=cos^2A. \Rightarrow S_{ASK}=S_{ABC}.cos^2A[/tex](đpcm).
Câu c em nghĩ là dấu [tex]\leq[/tex] đúng không ạ?
c) Dễ dang chứng minh được [tex]\Delta BHI\sim \Delta ACI(g-g) \Rightarrow \frac{IH}{IC}=\frac{IB}{IA}\Rightarrow IH.IA=IB.IC[/tex].
Lại có IB+IC= BC không đổi do tam giác ABC không đổi.
Do đó IB.IC[tex]\leq \frac{BC}{2}.\frac{BC}{2}=\frac{BC^2}{4}[/tex]
hay IH.IA [tex]\leq \frac{BC^2}{4}[/tex]
Dấu bằng xảy ra khi IB=IC nên i là trung điểm BC.Suy ra tam giác ABC cân tại A.
Mọi người xem có sai gì không ạ.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
