- 10 Tháng sáu 2017
- 660
- 794
- 131
- 21
- Phú Thọ
- THPT Thanh Thủy
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
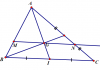
Cho tam giác ABC có G là trọng tâm, M là điểm trên cạnh AB sao cho [tex]\underset{MA}{\rightarrow}= -3\underset{MB}{\rightarrow}[/tex]. Điểm N thuộc cạnh AC: [tex]\underset{AN}{\rightarrow}=k.\underset{AC}{\rightarrow}[/tex].
Tìm K để M,G,N thẳng hàng
Tìm K để M,G,N thẳng hàng