Cho S.ABC đều cód(M,SAB)=a/4, M là trung điểm CB ((SAB),(SAC))=30°Tính V
Nguyễn Đặng Lan Anh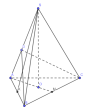
Gọi cạnh đáy là b, cạnh bên là c
ta có: [imath]d(M,(SAB))=\dfrac{a}{4}\Rightarrow d(O,(SAB))=\dfrac{a}{6}\Rightarrow d(O,(SBC))=\dfrac{a}{6}[/imath] (do S.ABC đều)
[imath]AO=\dfrac{b\sqrt3}{3}\Rightarrow SO=\sqrt{c^2-\dfrac{b^2}{3}}[/imath]
Hệ thức lượng trong tam giác SOM có
[imath]\dfrac{1}{d(O,(SBC))^2}=\dfrac{1}{OM^2}+\dfrac{1}{SO^2}[/imath]
[imath]\Rightarrow \dfrac{36}{a^2}=\dfrac{12}{b^2}+\dfrac{3}{3c^2-b^2}\Rightarrow \dfrac{12}{a^2}=\dfrac{4}{b^2}+\dfrac{1}{3c^2-b^2}[/imath]
Kẻ [imath]BD\bot SA; SK\bot AB[/imath]
[imath]SK=\sqrt{c^2-\dfrac{b^2}{4}}[/imath]
[imath]BD=\dfrac{SK.AB}{SA}=\dfrac{b\sqrt{c^2-\dfrac{b^2}{4}}}{c}[/imath]
[imath]\cos ((SAB),(SAC))=\cos \widehat{BDC}=\dfrac{BD^2+DC^2-BC^2}{2BD.DC}=1-\dfrac{BC^2}{2BD.DC}[/imath]
[imath]=1-\dfrac{b^2c^2}{2b^2(c^2-\dfrac{b^2}{4})}=1-\dfrac{2c^2}{4c^2-b^2}=\dfrac{2c^2-b^2}{4c^2-b^2}=\dfrac{\sqrt3}{2}[/imath]
Đến đây thì chị thấy vô nghiệm, em check lại đề và bài chị làm xem sao nha.
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm tại
Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
