[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
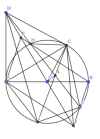
Cho (O) đường kính AB = 2R và một điểm M cố định trên tiếp tuyến của (O) tại A. Qua M kẻ tiếp tuyến MC và cát tuyến MHK với (O) ( C, H, K thuộc (O), H nằm giữa M và K, tia MK nằm giữa hai tia MB và MO. Các đường thẳng BH, BK cắt đường thẳng MO lần lượt tại E và F. Qua A kẻ đường thẳng song song với MK cắt đường tròn tại I. Nối CI cắt MK tại N.
- Chứng minh tứ giác MCHE nội tiếp
- Chứng minh OE = OF
- Chứng minh: MN2 + ON2 không phụ thuộc vào vị trí của cát tuyến MHK
- Tìm giá trị lớn nhất của diện tích tam giác MKI khi cát tuyến MHK thay đổi nhưng luôn nằm giữa hoặc trùng với hai tia MB và MO