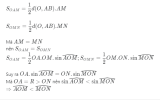[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho (O) có dây cung AB không đi qua tâm. Trên AB lấy 2 điểm M,N sao cho AM=MN=NB. Chứng minh rằng [imath]\widehat{AOM}<\widehat{MON}[/imath]
mn giúp e với ạ
mn giúp e với ạ
Last edited by a moderator: