Toán 12 Cho hình trụ có diện tích xung quanh và thể tích lần lượt là $160 \pi cm^2$ và $320 \pi cm^3$

[Lê Gia An]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

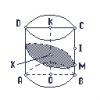
Cho hình trụ có diện tích xung quanh và thể tích lần lượt là $160 \pi cm^2$ và $320 \pi cm^3$. Thiết diện qua trục của hình trụ là hình chữ nhật $ABCD$ có các đường kính đáy lần lượt là $AB$ và $CD$. Gọi $I$ là trung điểm $BC$ và gọi $M$ là điểm di động trên $BI$. Biết rằng thiết diện của hình trụ qua $M$ là một elip có diện tích là $20\pi$ đồng thời chia khối trụ thành hai khối có tỉ lệ thể tích khối nhỏ trên khối lớn là $\dfrac{7}{13}$. Tính tỉ lệ $\dfrac{BM}{MC}$

Mọi người giúp em với

 

[iceghost]

Trước hết, mình xử lý dữ kiện dễ trước:

$S_{xq} = 2 \pi R \cdot h= 160\pi$

$V = \pi R^2 \cdot h = 320 \pi$

Giải hpt ta được $R = 4$ và $h = 20$

Tới đây, giả sử thiết diện qua $M$ cắt trục $OK$ tại $X$ thì ta sẽ có $\dfrac{XO}{XK} = \dfrac{7}{13}$ (mọi mặt phẳng đi qua $X$ đều chia đúng tỉ lệ này). Do $OK = 20$ nên $XO = 7$ và $XK = 13$ luôn, nó lại hợp lý

Tới đây bạn có bán kính trục nhỏ bằng $R$ và bán kính trục lớn bằng $XM$. Từ diện tích elip bạn sẽ tìm được $XM = 5$.

Tới đây bạn tìm ra được vị trí điểm $M$ dễ dàng thôi à: $MB = 4$, suy ra tỉ lệ cần tìm là $\dfrac{4}{16} = \dfrac{1}4$

Bạn tham khảo thử cách làm trên nha Chúc bạn học tốt!