Toán 8 Cho hình thang [imath]ABCD (AB \parallel CD, AB < CD)[/imath]

[Blacklead Gladys]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

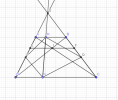
Cho hình thang [imath]ABCD (AB \parallel CD, AB < CD)[/imath]. Gọi [imath]I[/imath] là giao điểm của [imath]AC[/imath] và [imath]BD[/imath], đường thẳng qua [imath]I[/imath] song song với [imath]AB[/imath] cắt [imath]AD, BC[/imath] tại [imath]E[/imath] và [imath]F[/imath]
a. Chứng minh [imath]I[/imath] là trung điểm của [imath]EF[/imath]
b. Lấy [imath]M[/imath] thuộc [imath]AB, N[/imath] thuộc [imath]CD[/imath] sao cho [imath]\dfrac{AM}{BM} = \dfrac{DN}{CN}[/imath]. Gọi [imath]P, Q[/imath] là trung điểm của [imath]AD[/imath] và [imath]BC[/imath]. Chứng minh [imath]S_{MNPQ} = \dfrac{1}2 S_{ABCD}[/imath]
c. Chứng minh [imath]AD, BC, MN[/imath] đồng quy

mn giúp e bài hình này vs . ghi gợi ý cx đc ak

 

[Timeless time]

Có vẻ em đang cần gấp nên chị làm nhanh giúp em ý a trước nhé, @Cáp Ngọc Bảo Phương , @chi254 vào cứu ý b,c với

Em tự vẽ hình nhé
a. Xét tam giác [imath]ACD[/imath] có [imath]EI \parallel CD[/imath] nên suy ra : [imath]\dfrac{EI}{DC} = \dfrac{AI}{AC}[/imath] (định lý talet) [imath](1)[/imath]
Tương tự xét tam giác [imath]BCD[/imath] có : [imath]\dfrac{IF}{CD} = \dfrac{BI}{BD} \quad (2)[/imath]
Xét tam giác [imath]ABI[/imath] có: [imath]\dfrac{AI}{AC} = \dfrac{BI}{BD} \quad (3)[/imath]
Từ [imath](1),(2),(3)[/imath] suy ra : [imath]\dfrac{EI}{DC} = \dfrac{IF}{CD} \implies EI = IF \implies I[/imath] là trung điểm của [imath]EF[/imath]
Có gì không hiểu em hỏi lại nha
Ngoài ra em có thể tham khảo thêm kiến thức tại đây nhé

 

[Alice_www]

b) Gọi h là chiều cao hình thang
[imath]S_{APM}=\dfrac12 \dfrac{h}{2}AM[/imath]
[imath]S_{QBM}=\dfrac12 \dfrac{h}{2} BM[/imath]
Suy ra [imath]S_{APM}+S_{QBM}=\dfrac14 h.AB[/imath]
CMTT ta có [imath]S_{PDN}+S_{QNC}=\dfrac14 hDC[/imath]
Suy ra [imath]S_{APM}+S_{QBM}+S_{PDN}+S_{QNC}= \dfrac14 h.(AB+DC)=\dfrac{S_{ABCD}}{2}[/imath]
[imath]S_{MPNQ}=S_{ABCD}-(S_{APM}+S_{QBM}+S_{PDN}+S_{QNC})=\dfrac{S_{ABCD}}{2}[/imath]

c.
không mất tính tổng quát giả sử [imath]\dfrac{AM}{BM}=\dfrac{DN}{CN}<1[/imath]
Gọi [imath]G=AD\cap MN[/imath]
[imath]AM//DN\Rightarrow \dfrac{GM}{GN}=\dfrac{AM}{DN}[/imath]
Gọi [imath]G'=BC\cap MN[/imath]
[imath]MB//NC \Rightarrow \dfrac{G'M}{G'N}=\dfrac{MB}{NC}[/imath]
Mà [imath]\dfrac{AM}{DN}=\dfrac{BM}{CN}[/imath]
Suy ra [imath]\dfrac{GM}{GN}=\dfrac{G'M}{G'N}[/imath]
[imath]\Rightarrow \dfrac{GM}{MN}=\dfrac{G'M}{MN}[/imath]
[imath]\Rightarrow GM=G'M[/imath]
Mà [imath]G;G'[/imath] nằm cùng phía và trên đoạn [imath]MN[/imath]
nên [imath]G\equiv G'[/imath]
Vậy [imath]AD;BC;MN[/imath] đồng quy

Có gì khúc mắc em hỏi lại nhé
Ngoài ra em có thể tham khảo thêm các kiến thức tại: https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397