[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
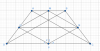
Cho hình thang cân $ABCD (AB \parallel CD)$. Gọi $M,N,P,Q$ lần lượt là trung điểm của các cạnh $AB,BC,CD,DA$
a. Chứng minh $MP$ là phân giác của góc $\widehat{QMN}$
b. Hình thang $ABCD$ phải có thêm điều kiện gì đối với hai đường chéo để góc $\widehat{MNQ}=45^\circ$
c. Chứng minh rằng nếu có thêm điều kiện của câu b thì hình thang cân $ABCD$ có đường cao bằng đường trung bình của nó
mn giúp e bài 2 ggaps vs ạ
a. Chứng minh $MP$ là phân giác của góc $\widehat{QMN}$
b. Hình thang $ABCD$ phải có thêm điều kiện gì đối với hai đường chéo để góc $\widehat{MNQ}=45^\circ$
c. Chứng minh rằng nếu có thêm điều kiện của câu b thì hình thang cân $ABCD$ có đường cao bằng đường trung bình của nó
mn giúp e bài 2 ggaps vs ạ
Attachments
Last edited by a moderator: