[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
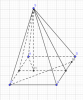
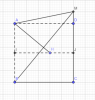
Cho hình chóp S.ABCD đáy là hình vuông cạnh a; mặt bên tam giác SAB là tam giác đều;
tam giác SCD vuông cân đỉnh S; hai điểm I,J là trung điểm AB, CD
a, Tính các cạnh của tam giác SIJ. Chứng minh: SI vuông (SCD)
b,Gọi H là hình chiếu vuông góc của S trên IJ. Chứng minh: SH vuông AC
c, Cho M thuộc CD sao cho BM vuông SA. Tính AM theo a
Em còn câu c chưa làm được, giúp em với ah
tam giác SCD vuông cân đỉnh S; hai điểm I,J là trung điểm AB, CD
a, Tính các cạnh của tam giác SIJ. Chứng minh: SI vuông (SCD)
b,Gọi H là hình chiếu vuông góc của S trên IJ. Chứng minh: SH vuông AC
c, Cho M thuộc CD sao cho BM vuông SA. Tính AM theo a
Em còn câu c chưa làm được, giúp em với ah
Last edited by a moderator: