Cho hai đường tròn C1(O1; R1); C2(O2; R2) tiếp xúc ngoài nhau tại A. Hai điểm B và C lần lượt di động trên hai đường tròn sao cho góc BAC = 90 độ.
a) Chứng minh rằng trung điểm M của BC luôn thuộc đường tròn cố định
b) Hạ AH vuông góc với BC, tìm tập hợp các điểm H. Chứng minh rằng độ dài của đoạn AH không lớn hơn [math]\frac{2R1.R2}{R1+R2}[/math]
doanhnhannguyenthinh@gmail.com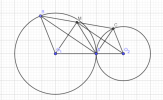
a)
Gọi [imath]\widehat{BO_1A}=\alpha; \widehat{AO_2C}=\beta[/imath]
[imath]\alpha +\beta+2\widehat{O_1AB}+2\widehat{CAO_2}=360^\circ\Rightarrow \alpha+\beta=180^\circ[/imath]
[imath]MA=MB; O_1A=O_1B\Rightarrow O_1M[/imath] là đường trung trực của AB
[imath]\Rightarrow \widehat{MO_1A}=\widehat{MO_1B}[/imath]
Tương tự ta có [imath]\widehat{AO_2M}= \widehat{CO_2M}[/imath]
Suy ra [imath]\widehat{MO_1A}+ \widehat{MO_2A}=\dfrac{\alpha+\beta}2=90^\circ[/imath]
[imath]\Rightarrow \widehat{O_1MO_2}=90^\circ\Rightarrow M[/imath] thuộc đường tròn đường kính [imath]O_1O_2[/imath] cố định
b) [imath]AB^2=2R_1^2-2R_1^2\cos \alpha=R_1^2\cos^2 \dfrac{\alpha}2\Rightarrow AB=2R_1\cos \dfrac{\alpha}2[/imath]
Tương tự ta có: [imath]AC=2R_2\cos \dfrac{\beta}2[/imath]
[imath]\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}\le \dfrac{2R_1R_2}{R_1+R_2}[/imath]
[imath]\Rightarrow 2\cos \dfrac{\alpha}2\cos \dfrac{\beta}2(R_1+R_2)\le \sqrt{AB^2+AC^2}[/imath]
[imath]\Rightarrow \cos^2 \dfrac{\alpha}2\cos^2 \dfrac{\beta}2 (R_1^2+2R_1R_2+R_2^2)\le R_1^2 \cos^2 \dfrac{\alpha}2+R_2^2\cos^2 \dfrac{\beta}2[/imath]
[imath]\Rightarrow R_1^2 \cos^2 \dfrac{\alpha}2\sin^2\dfrac{\beta}2-2R_1R_2\cos^2 \dfrac{\alpha}2\cos^2 \dfrac{\beta}2+R_2^2\cos^2 \dfrac{\beta}2\sin ^2\dfrac{\alpha}2\ge 0[/imath]
[imath]\Rightarrow \left(R_1\cos ^2 \dfrac{\alpha}2-R_2\cos^2 \dfrac{\beta}2\right)^2\ge 0[/imath] (luôn đúng)
Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại
Đường tròn
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


