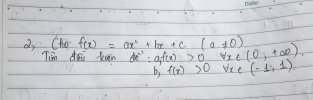Toán 10 Cho $f(x)=ax^2+bx+c$

[Mẫu Đơn]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho [imath]f(x) = ax^2 + bx + c (a \ne 0)[/imath]
Tìm điều kiện để
a) [imath]f(x) > 0 \ \ \forall x \in (0; +\infty)[/imath]
b) [imath]f(x) > 0 \ \ \forall x \in (-1;1)[/imath]

Mong mn có thể giúp đỡ!!

 

[chi254]

Cho [imath]f(x) = ax^2 + bx + c (a \ne 0)[/imath]
Tìm điều kiện để
a) [imath]f(x) > 0 \ \ \forall x \in (0; +\infty)[/imath]
b) [imath]f(x) > 0 \ \ \forall x \in (-1;1)[/imath]

Mong mn có thể giúp đỡ!!

Mẫu Đơn
a) ĐK cần: [imath]a > 0[/imath]
TH1: [imath]f(x) = 0[/imath] vô nghiệm thì [imath]f(x) > 0 \ \ \forall x \in \R[/imath]
Hay [imath]\Delta < 0 \iff b^2 - 4ac <0[/imath]
TH2: [imath]f(x) = 0[/imath] có nghiệm kép thì [imath]b^2 - 4ac = 0[/imath]
ĐK: [imath](0;+\infty) \sub \left ( \dfrac{-b}{2a} ; +\infty \right)[/imath]
[imath]\iff \dfrac{-b}{2a} \le 0[/imath]
[imath]\iff b \ge 0[/imath]
TH3: [imath]f(x) = 0[/imath] có 2 nghiệm phân biệt [imath]x_1; x_2[/imath]
Để [imath]f(x) > 0 \ \ \forall x \in (0;+\infty)[/imath] thì [imath](0;+\infty) \sub \left ( x_2 ; +\infty \right)[/imath]
[imath]\iff x_1 < x_2 < 0 \iff \begin{cases} af(0) > 0 \\ S = \dfrac{-b}{a} < 0 \end{cases}[/imath]
b) Chia trường hợp tương tự em nhé


Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo kiến thức tại Tổng hợp sách giáo khoa mới