Toán 9 Cho đường tròn (O) đường kính AB.

[phúck7]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho đường tròn (O) đường kính AB. Từ điểm M (điểm M khác điểm A) trên tiếp tuyến Ax của đường tròn vẽ tiếp tuyến thứ hai MC (C là tiếp điểm). Từ điểm C vẽ CH vuông góc với AB (H ∈ AB); MB cắt đường tròn tâm (O) tại điểm Q (điểm Q khác điểm B) và cắt CH tại điểm N; MO cắt AC tại điểm I a) Chứng minh AIQM là tứ giác nội tiếp b) Chứng minh CH=2CN​

 

[Lê Minh Huyền]

bạn tự vẽ hình nha
(bài mình tự làm, bạn tham khảo nha)

a. MB cắt IC tại P
- tam giác IPQ đồng dạng với tg NPC
=> góc IQP = góc NCP (1)
- lại có tam giác ACB vuông tại C, chiều cao CH
=> góc ACH ( = PCN) = góc CBA (cùng phụ với góc BAC) (2)
Mà góc CBA = MAC (cùng chắn cung AC) (3)
Từ (1),(2),(3) => góc IQP = góc MAC
=> AIQM là tứ giác nội tiếp

 

[Nguyễn Đình Trường]

Cho đường tròn (O) đường kính AB. Từ điểm M (điểm M khác điểm A) trên tiếp tuyến Ax của đường tròn vẽ tiếp tuyến thứ hai MC (C là tiếp điểm). Từ điểm C vẽ CH vuông góc với AB (H ∈ AB); MB cắt đường tròn tâm (O) tại điểm Q (điểm Q khác điểm B) và cắt CH tại điểm N; MO cắt AC tại điểm I a) Chứng minh AIQM là tứ giác nội tiếp b) Chứng minh CH=2CN​

phúck7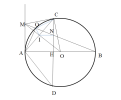
Gọi D là giao điểm của CH và (O) => ACH=ADH(1)
+) Ta có MA=MC và OA=OC => OM là trung trực của AC => CI = IA (*)
+) AIQM nội tiếp => MAC=IQN (...) (2)
+) AM là tiếp tuyến => MAC=ADH (...) (3)
+) Từ (1)(2) và (3) => ACH= IQN hay ICN=IQN => IQCN nội tiếp
=>CQN=CIN mà CQN=CAH ( chắn BC )
=>CIN=CAH => Tam giác CIN đồng dạng với CAH =>CNI=CHA=90 độ => IN//AH(**)
+) Từ (*) và (**) => IN là đường trung bình tam giác CAH => CN=HN hay CH=2CN

Bn xem lại hộ mình xem mình làm có sai chỗ nào k
với lại mk lm hơi tắt phần giải thích nha