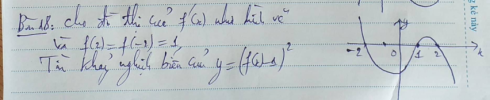[imath]y'=2f'(x).(f(x)-1)[/imath]
Từ đồ thị của [imath]f'(x)[/imath] có thể duy được [imath]f(x)[/imath] đạt [imath]\max[/imath] tại [imath]2[/imath] điểm cực đại là [imath]x=2[/imath] và [imath]x=-2[/imath], điều này tức là [imath]\max f(x) = f(-2)=f(2)=1[/imath]
Vậy [imath]f(x)-1 \leq 0[/imath] [imath]\forall x \in \mathbb{R}[/imath]
Vậy các khoảng nghịch biến của [imath]y=(f(x)-1)^2[/imath] là các khoảng mà tại đó [imath]f'(x)>0[/imath] đó là [imath](-\infty, -2)[/imath] hoặc [imath](1,2)[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.