Toán 9 Cho $\Delta ABC$ có $AB =\sqrt{2}$

[minh123@]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

giúp em vs ạ !!
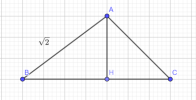
Cho [imath]\Delta ABC[/imath] có [imath]AB =\sqrt{2} ; \widehat{BAC} = 60^o; \widehat{ACB} = 45^o[/imath]. Vẽ các đường cao [imath]AH;BK[/imath] của [imath]\Delta ABC[/imath]
a) Tính [imath]BK;CK;BH;CH[/imath]
b) Từ các kết quả trên hãy tính [imath]\sin 15^o[/imath]

 

[Alice_www]

giúp em vs ạ !!
Cho [imath]\Delta ABC[/imath] có [imath]AB =\sqrt{2} ; \widehat{BAC} = 60^o; \widehat{ACB} = 45^o[/imath]. Vẽ các đường cao [imath]AH;BK[/imath] của [imath]\Delta ABC[/imath]
a) Tính [imath]BK;CK;BH;CH[/imath]
b) Từ các kết quả trên hãy tính [imath]\sin 15^o[/imath]

minh123@
[imath]\widehat{ABC}=180^\circ-\widehat{BAC}-\widehat{ACB}=75^\circ[/imath]

[imath]\cos \widehat{ABC}=\dfrac{AH}{AB}\Rightarrow AH=AB.\cos \widehat{ABC}=\dfrac{-1+\sqrt3}2[/imath]

Áp dụng định lí sin cho [imath]\Delta ABC[/imath] ta có:

[imath]\dfrac{AB}{\sin \widehat{ACB}}=\dfrac{AC}{\sin \widehat{ABC}}=\dfrac{BC}{\widehat{BAC}}=2[/imath]

[imath]\Rightarrow AC=\dfrac{\sqrt6+\sqrt2}2; BC=\sqrt3[/imath]

[imath]2S=BK.AC=AH.BC\Rightarrow BK=\dfrac{AH.BC}{AC}=\dfrac{2\sqrt6-3\sqrt2}{2}[/imath]

[imath]CK=\sqrt{BC^2-BK^2}=\sqrt{\dfrac{-15+12\sqrt3}2}[/imath]

[imath]BH=\sqrt{AB^2-AH^2}=\dfrac{1+\sqrt3}2; CH=CB-BH=\dfrac{-1+\sqrt3}2[/imath]

Ta có [imath]AH=CH\Rightarrow \Delta AHC[/imath] vuông cân tại H
[imath]\Rightarrow \widehat{HAC}=45^\circ[/imath]
[imath]\Rightarrow \widehat{BAH}=\widehat{BAC}-\widehat{HAC}=15^\circ[/imath]

[imath]\sin \widehat{BAH}=\sin 15^\circ=\dfrac{AH}{AB}=\dfrac{\sqrt6-\sqrt2}4[/imath]

Có gì khúc mắc em hỏi lại nha
Ngoài ra, em xem thêm tại Ôn tập toán các dạng bài hình học 9