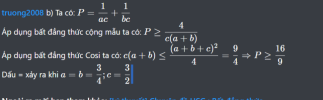[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
a, Cho a,b thỏa mãn: (a+b)^3 + 2ab<=10. Tìm GTLN của Q = 1/(a+1) + 1/(b+1) + 2020ab
b, cho a,b,c>0 và a+b+c=3. Tìm GTNN của P= (a+b)/abc
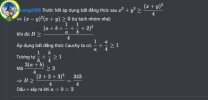
c, cho a,b,c là các số thực dương và a+b=4. Tìm GTNN của B=(a+1/a+1)^3 + (b+1/b+1)^3
Mn giúp e với ạ. Nếu được thì mn chỉ em phương pháp làm mấy bài này với ạ! Em cảm ơn
anh ơi anh lm ra giấy rồi gửi e đc ko ạ máy e ko xem đc latex
b, cho a,b,c>0 và a+b+c=3. Tìm GTNN của P= (a+b)/abc
c, cho a,b,c là các số thực dương và a+b=4. Tìm GTNN của B=(a+1/a+1)^3 + (b+1/b+1)^3
Mn giúp e với ạ. Nếu được thì mn chỉ em phương pháp làm mấy bài này với ạ! Em cảm ơn
anh ơi anh lm ra giấy rồi gửi e đc ko ạ máy e ko xem đc latex
Last edited: