 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào các bạn ^^
Hôm nay mình sẽ chia sẻ với các bạn về cách vẽ Đồ thị hàm số chứa dấu giá trị tuyệt đối nhé ^^
Mình sẽ ví dụ một đồ thị trước nhé ^^
Ta sẽ làm như sau :
Bước 1: Vẽ đường thẳng $y = 2x + 4$ với phần đồ thị sao cho $x \ge \frac{-4}{2}=-2$ gọi là $(d_1)$
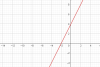
Bước 2: Vẽ đường thẳng $y = -2x - 4$ với phần đồ thị sao cho $x < \frac{4}{-2}=-2$ gọi là $(d_2)$
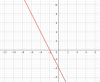
Bước 3: Lấy hợp của hai đồ thị $(d_1)$ và $(d_2)$ ta được đồ thị của hàm số [tex]y=|2x+4|[/tex]

Vậy qua ví dụ trên ta rút ra được cách vẽ như sau :
Yêu cầu : Vẽ đồ thị của hàm số sau : [tex]y=|ax+b|[/tex]
Bước 1: Vẽ đường thẳng $y = ax+b$ với phần đồ thị sao cho $x \ge \frac{-b}{a}$ gọi là $(d_1)$
Bước 2: Vẽ đường thẳng $y = -ax-b$ với phần đồ thị sao cho $x < \frac{-b}{a}$ gọi là $(d_2)$
Bước 3: Lấy hợp của hai đồ thị $(d_1)$ và $(d_2)$ ta được đồ thị của hàm số [tex]y=|ax+b|[/tex]
Chúng ta cùng đến với các ví dụ sau nhé^^
Ví dụ 1: Vẽ đồ thị của hàm số sau : [tex]y=|x|-5[/tex]
+,Vẽ đường thẳng $y = x-5$ với phần đồ thị sao cho $x \ge 0$ gọi là $(d_1)$
+,Vẽ đường thẳng $y = -x-5$ với phần đồ thị sao cho $x < 0$ gọi là $(d_2)$
+,Lấy hợp của hai đồ thị $(d_1)$ và $(d_2)$ ta được đồ thị của hàm số [tex]y=|x|-5[/tex]

Ồ, nhìn đồ thị này ta có thể thấy 2 đường thẳng $(d_1)$ và $(d_2)$ đối xứng nhau qua trục tung, do đó ta có thêm 1 mẹo để vẽ thêm đồ thị dạng $y=|ax|+b$ (không mát tính tổng quát giả sử $a \ge 0$) là :
Bước 1 : Vẽ đường thẳng $y = ax+b$ với phần đồ thị sao cho $x \ge 0$ gọi là $(d_1)$
Bước 2 : Lấy đối xứng của đường thẳng $(d_1)$ qua trục tung ta được đường thẳng $(d_2)$
Ví dụ 2: Vẽ đồ thị của hàm số sau : [tex]y=||x|-5|[/tex]
Cách làm tương tự như trên , ta được đồ thị :

Ví dụ 3: Vẽ đồ thị của hàm số sau : [tex]y=|x-3|+|x+1| [/tex]
Ta có bẳng xét dấu như sau :
[TBODY]
[/TBODY]Cách vẽ tương tự trên ta được đồ thị :

Topic của mình tới đây là hết rồi . Hy vọng qua topic này có thể giúp các bạn vẽ đồ thi hàm số chứa dấu giá trị tuyệt đối một cách dễ dàng hơn ^^
Cảm ơn các bạn đã đọc bài viết này!
Hôm nay mình sẽ chia sẻ với các bạn về cách vẽ Đồ thị hàm số chứa dấu giá trị tuyệt đối nhé ^^
Mình sẽ ví dụ một đồ thị trước nhé ^^
Ta sẽ làm như sau :
Bước 1: Vẽ đường thẳng $y = 2x + 4$ với phần đồ thị sao cho $x \ge \frac{-4}{2}=-2$ gọi là $(d_1)$

Bước 2: Vẽ đường thẳng $y = -2x - 4$ với phần đồ thị sao cho $x < \frac{4}{-2}=-2$ gọi là $(d_2)$

Bước 3: Lấy hợp của hai đồ thị $(d_1)$ và $(d_2)$ ta được đồ thị của hàm số [tex]y=|2x+4|[/tex]

Vậy qua ví dụ trên ta rút ra được cách vẽ như sau :
Yêu cầu : Vẽ đồ thị của hàm số sau : [tex]y=|ax+b|[/tex]
Bước 1: Vẽ đường thẳng $y = ax+b$ với phần đồ thị sao cho $x \ge \frac{-b}{a}$ gọi là $(d_1)$
Bước 2: Vẽ đường thẳng $y = -ax-b$ với phần đồ thị sao cho $x < \frac{-b}{a}$ gọi là $(d_2)$
Bước 3: Lấy hợp của hai đồ thị $(d_1)$ và $(d_2)$ ta được đồ thị của hàm số [tex]y=|ax+b|[/tex]
Chúng ta cùng đến với các ví dụ sau nhé^^
Ví dụ 1: Vẽ đồ thị của hàm số sau : [tex]y=|x|-5[/tex]
+,Vẽ đường thẳng $y = x-5$ với phần đồ thị sao cho $x \ge 0$ gọi là $(d_1)$
+,Vẽ đường thẳng $y = -x-5$ với phần đồ thị sao cho $x < 0$ gọi là $(d_2)$
+,Lấy hợp của hai đồ thị $(d_1)$ và $(d_2)$ ta được đồ thị của hàm số [tex]y=|x|-5[/tex]
Ồ, nhìn đồ thị này ta có thể thấy 2 đường thẳng $(d_1)$ và $(d_2)$ đối xứng nhau qua trục tung, do đó ta có thêm 1 mẹo để vẽ thêm đồ thị dạng $y=|ax|+b$ (không mát tính tổng quát giả sử $a \ge 0$) là :
Bước 1 : Vẽ đường thẳng $y = ax+b$ với phần đồ thị sao cho $x \ge 0$ gọi là $(d_1)$
Bước 2 : Lấy đối xứng của đường thẳng $(d_1)$ qua trục tung ta được đường thẳng $(d_2)$
Ví dụ 2: Vẽ đồ thị của hàm số sau : [tex]y=||x|-5|[/tex]
Cách làm tương tự như trên , ta được đồ thị :

Ví dụ 3: Vẽ đồ thị của hàm số sau : [tex]y=|x-3|+|x+1| [/tex]
Ta có bẳng xét dấu như sau :
| x | -1 | 3 | |||
| y | -2x+2 | || | 4 | || | 2x-2 |

Topic của mình tới đây là hết rồi . Hy vọng qua topic này có thể giúp các bạn vẽ đồ thi hàm số chứa dấu giá trị tuyệt đối một cách dễ dàng hơn ^^
Cảm ơn các bạn đã đọc bài viết này!


