- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Đây vốn là một dạng bài dễ, sau đây mình xin trình bày cách hạ gục dạng bài này một cách dễ dàng.
Dạng 1. Phân tích một vectơ tùy ý theo hai vectơ trên cạnh của tam giác.
Ý tưởng: Để phân tích $\vec{MN}$ theo $\vec{AB}$ và $\vec{AC}$, ta đưa $\vec{MN} = \vec{AN} - \vec{AM}$ rồi phân tích từng vectơ thành phần theo hai vectơ đề cho.
Bước 1. Chuyển các giả thuyết về dạng vectơ.
Bước 2. Chèn điểm vào các giả thuyết để tính vectơ thành phần.
Bước 3. Dùng hiệu hai vectơ để tính vectơ đề yêu cầu.
Nếu vectơ cần tính có một đầu là đỉnh tam giác, $\vec{AM}$ chẳng hạn, thì tất nhiên công việc sẽ nhẹ nhàng hơn.
Ví dụ 1. Cho $\triangle{ABC}$, $G$ là trọng tâm, $I$ là điểm trên đoạn $BC$ sao cho $2CI = 3BI$, $J$ là điểm trên $BC$ kéo dài thỏa $7JB = 4JC$. Tính $\vec{AI}$, $\vec{AJ}$, $\vec{AG}$, $\vec{JG}$ theo $\vec{AB}$, $\vec{AC}$.
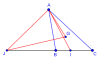
Nhận xét. Thực ra đề vạch sẵn đường đi cho mình luôn rồi, nhưng nếu đề chỉ yêu cầu tính $\vec{JG}$ thì bạn cũng nên tự hiểu là phải đi tính $\vec{AJ}$ với $\vec{AG}$ nhé.
Giải. $2CI = 3BI \implies 2\vec{CI} = -3\vec{BI}$ (ngược hướng)
$\implies 2\vec{CA} + 2 \vec{AI} = -3\vec{BA} - 3\vec{AI}$
$\implies 5\vec{AI} = -3\vec{BA} - 2\vec{CA}$
$\implies \vec{AI}=\dfrac{3}5\vec{AB}+\dfrac{2}5\vec{AC}$
$7JB = 4JC \implies 7\vec{JB} = 4\vec{JC}$ (cùng hướng)
$\implies 7\vec{JA} + 7\vec{AB} = 4\vec{JA} + 4\vec{AC}$
$\implies 3\vec{JA} = -7\vec{AB} + 4\vec{AC}$
$\implies \vec{AJ} = \dfrac{7}3\vec{AB}-\dfrac{4}3\vec{AC}$
$\vec{AG}=\dfrac13\vec{AA}+\dfrac13\vec{AB}+\dfrac13\vec{AC}$ (quy tắc trọng tâm)
$=\dfrac13\vec{AB}+\dfrac13\vec{AC}$
$\vec{JG}=\vec{AG}-\vec{AJ}=-2\vec{AB}+\dfrac{5}3\vec{AC}$
Dạng 2. Phân tích một vectơ tùy ý theo hai vectơ bất kỳ khác
Dạng này cần phối hợp nhiều bài toán dạng 1. Chẳng hạn đề bảo phân tích $\vec{a}$ theo $\vec{b}$ và $\vec{c}$, ý tưởng như sau:
- Phân tích $\vec{a}$ theo hai vectơ trên cạnh của tam giác như $\vec{AB}$, $\vec{AC}$ giống dạng 1.
- Làm tương tự với $\vec{b}$ và $\vec{c}$.
- Giả sử ta phân tích được $\vec{a} = x\vec{b} + y\vec{c}$, việc bây giờ là tìm $x$ và $y$. Thay các biểu thức tìm được ở trên xuống dưới, đơn giản rồi giải hệ tìm ra $x$ và $y$.
Sang ví dụ sau đây sẽ rõ hơn cách làm:
Ví dụ 2. Từ Ví dụ 1, phân tích $\vec{AI}$ theo $\vec{AJ}$ và $\vec{AG}$.
Nhận xét. Nếu như không có Ví dụ 1 mà đề bắt các bạn phân tích Ví dụ 2 luôn thì các bạn cũng phải hiểu ngầm là phải làm thêm Ví dụ 1 nhé.
Giải. Ta có $\vec{AI}=\dfrac{3}5\vec{AB}+\dfrac{2}5\vec{AC}$
$\vec{AJ} = \dfrac{7}3\vec{AB}-\dfrac{4}3\vec{AC}$
$\vec{AG}=\dfrac13\vec{AB}+\dfrac13\vec{AC}$
Giả sử ta phân tích được $\vec{AI} = x\vec{AJ} + y\vec{AG}$
$\implies \dfrac{3}5\vec{AB}+\dfrac{2}5\vec{AC} = \dfrac{7x}3\vec{AB}-\dfrac{4x}3\vec{AC} + \dfrac{y}3\vec{AB}+\dfrac{y}3\vec{AC}$
$\implies \dfrac{3}5\vec{AB}+\dfrac{2}5\vec{AC} = \left(\dfrac{7x}3 + \dfrac{y}3\right) \vec{AB} + \left(-\dfrac{4x}3+\dfrac{y}3\right)\vec{AC}$
$\implies \begin{cases} \dfrac{3}5 = \dfrac{7x}3 + \dfrac{y}3 \\ \dfrac{2}5 = -\dfrac{4x}3+\dfrac{y}3 \end{cases}$
$\implies \begin{cases} x = \dfrac{3}{55} \\ y = \dfrac{78}{55} \end{cases}$
Vậy $\vec{AI}=\dfrac{3}{55}\vec{AJ}+\dfrac{78}{55}\vec{AG}$
Lời kết. Hy vọng qua bài viết trên đây, bạn sẽ không còn sợ dạng bài phân tích một vectơ theo hai vectơ nữa. Thành thục kỹ năng phân tích vectơ sẽ giúp bạn tán đổ hầu hết các dạng bài vectơ. Thôi, hẹn gặp các bạn ở các bài viết tiếp theo nhé!
