- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạng bài pp tọa độ không gian xuất hiện trong đề thi đại học với số lượng câu hỏi khoảng 5-6 câu. Theo mình thấy thì đây là dạng bài làm tự luận thì khá lâu, nhưng khi làm trắc nghiệm thì có những cách loại trừ và thử đáp án nhanh, giúp cho các bạn có thể tiết kiệm thời gian để làm các câu khác.
Để áp dụng thì ít nhất các bạn phải biết những kiến thức cơ bản nhất về pp tọa độ, và không khuyến khích làm theo khi mới học chương này. Tốt nhất cứ tự làm cách tự luận đã, rồi vào đề thi thì sẽ tự biết cách làm trắc nghiệm. Sau đây là 1 số ví dụ về chính đề thi bộ đã ra 2 năm gần đây. Mình chỉ trình bày cách chọn đáp án nhanh chóng.
Câu này nằm trong đề thi 2018. Phân tích yêu cầu, đường thẳng qua A đó nó phải vuông góc d. Vậy chí ít tích vô hướng của vtcp d và vtcp của đường thẳng d' cần tìm, phải bằng 0. Đây là kiến thức hết sức cơ bản.
Bằng nhẩm tính rồi trực quan thì chỉ có A và B là 2 đáp án đã thỏa mãn điều này.
Tiếp đến xét sự cắt trục Ox, cơ bản thì khi cắt Ox thì giao điểm có tọa độ dạng (x;0;0)
Vậy ở A thử luôn t=0 được y=z=0. Đồng thời t=1 thấy thỏa mãn qua A, vậy A chính là đáp án
1 câu tiếp theo trong đề 2018 , 1 dạng cơ bản về nhìn đáp án mà loại.
Với dạng cho các pt đường thẳng thế này, ta xem 4 đáp án, nếu có 3 vtcp giống nhau và 1 khác thì đáp án khác đấy loại luôn. Trường hợp chia 2:2 thì không loại được ngay, nhưng với chia 2:1:1 này thì loại luôn 2 đáp án A và D đi. Thử B và C thôi .
B và C chỉ khác nhau ở điểm đi qua. Giờ rõ ràng rằng, đường phân giác phải đi qua giao điểm A' của delta và d. Vậy ta chỉ cần giải tìm tọa độ A' rồi thay thử vào đáp án, nếu A' thuộc đường thẳng thì đáp án đúng, không thuộc thì loại, chọn đáp án còn lại
Câu này lại càng không phải giải, vì rõ ràng thấy A đã thuộc d, mà A thuộc delta nữa, nên A chính là giao điểm A' cần tìm
Thay thử vào B thấy không thỏa mãn, do đó chọn C
Tiếp theo là một câu trong đề năm 2017, lại tiếp tục vuông góc các thứ thì cứ tích vô hướng của 2 vtcp bằng 0 thôi. Nhìn qua 4 đáp án thì lại chia tỉ lệ 2:1:1, vậy B hoặc D là đáp án. Nếu cẩn thận thêm tí thì các bạn có thể nhân thử sẽ thấy tích vô hướng = 0. Rồi giờ đi qua M, rõ ràng nhận ra ngay đường thẳng đáp án D đi qua M. Vậy câu này chọn D, 20s nhanh gọn
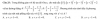
Một câu khác trong đề thi 2017, tiếp tục nhìn 4 đáp án. Nếu như ở dạng chọn đáp án ptdt thì ta quan tâm vtcp u, thì ở ptmp ta quan tâm vtpt n. Quan sát A và D là 2 đáp án có cùng vtpt, B và C thì khác nhau, vậy A hoặc D là đáp án
Việc còn lại chỉ là thử điều kiện tiếp xúc bằng cách tính khoảng các từ tâm I của S đến mp xem có bằng R hay không. Thử vào A thấy bằng luôn => Nhận .
Tiếp 1 câu đề 2017. Lại nhìn đáp án thấy có A và D là giống vtcp, B và C khác , nên A hoặc D đúng thôi. Giờ lại có A thuộc D, dễ dàng nhận ra rất nhanh. Vậy xong, D là đáp án
Qua vài ví dụ trên chắc bạn nào chưa biết thì cũng đã hiểu cách chọn đáp án nhanh này. Dạng bài pp tọa độ không gian, việc ra đề mà bị học sinh thử đáp án là khó tránh khỏi. Nên các bạn cứ yên tâm học chắc "CƠ BẢN" là đủ đã có đất diễn cho các bạn chọn đáp án rồi! Lưu ý 1 lần nữa là các bạn ở nhà luyện theo chuyên đề thì cứ giải tay, đừng ỷ lại kiểu này, mà không nắm vững kiến thức cơ bản là vẫn khó chọn nhanh lắm.
Để áp dụng thì ít nhất các bạn phải biết những kiến thức cơ bản nhất về pp tọa độ, và không khuyến khích làm theo khi mới học chương này. Tốt nhất cứ tự làm cách tự luận đã, rồi vào đề thi thì sẽ tự biết cách làm trắc nghiệm. Sau đây là 1 số ví dụ về chính đề thi bộ đã ra 2 năm gần đây. Mình chỉ trình bày cách chọn đáp án nhanh chóng.
Câu này nằm trong đề thi 2018. Phân tích yêu cầu, đường thẳng qua A đó nó phải vuông góc d. Vậy chí ít tích vô hướng của vtcp d và vtcp của đường thẳng d' cần tìm, phải bằng 0. Đây là kiến thức hết sức cơ bản.
Bằng nhẩm tính rồi trực quan thì chỉ có A và B là 2 đáp án đã thỏa mãn điều này.
Tiếp đến xét sự cắt trục Ox, cơ bản thì khi cắt Ox thì giao điểm có tọa độ dạng (x;0;0)
Vậy ở A thử luôn t=0 được y=z=0. Đồng thời t=1 thấy thỏa mãn qua A, vậy A chính là đáp án
1 câu tiếp theo trong đề 2018 , 1 dạng cơ bản về nhìn đáp án mà loại.
Với dạng cho các pt đường thẳng thế này, ta xem 4 đáp án, nếu có 3 vtcp giống nhau và 1 khác thì đáp án khác đấy loại luôn. Trường hợp chia 2:2 thì không loại được ngay, nhưng với chia 2:1:1 này thì loại luôn 2 đáp án A và D đi. Thử B và C thôi .
B và C chỉ khác nhau ở điểm đi qua. Giờ rõ ràng rằng, đường phân giác phải đi qua giao điểm A' của delta và d. Vậy ta chỉ cần giải tìm tọa độ A' rồi thay thử vào đáp án, nếu A' thuộc đường thẳng thì đáp án đúng, không thuộc thì loại, chọn đáp án còn lại
Câu này lại càng không phải giải, vì rõ ràng thấy A đã thuộc d, mà A thuộc delta nữa, nên A chính là giao điểm A' cần tìm
Thay thử vào B thấy không thỏa mãn, do đó chọn C
Tiếp theo là một câu trong đề năm 2017, lại tiếp tục vuông góc các thứ thì cứ tích vô hướng của 2 vtcp bằng 0 thôi. Nhìn qua 4 đáp án thì lại chia tỉ lệ 2:1:1, vậy B hoặc D là đáp án. Nếu cẩn thận thêm tí thì các bạn có thể nhân thử sẽ thấy tích vô hướng = 0. Rồi giờ đi qua M, rõ ràng nhận ra ngay đường thẳng đáp án D đi qua M. Vậy câu này chọn D, 20s nhanh gọn
Một câu khác trong đề thi 2017, tiếp tục nhìn 4 đáp án. Nếu như ở dạng chọn đáp án ptdt thì ta quan tâm vtcp u, thì ở ptmp ta quan tâm vtpt n. Quan sát A và D là 2 đáp án có cùng vtpt, B và C thì khác nhau, vậy A hoặc D là đáp án
Việc còn lại chỉ là thử điều kiện tiếp xúc bằng cách tính khoảng các từ tâm I của S đến mp xem có bằng R hay không. Thử vào A thấy bằng luôn => Nhận .
Tiếp 1 câu đề 2017. Lại nhìn đáp án thấy có A và D là giống vtcp, B và C khác , nên A hoặc D đúng thôi. Giờ lại có A thuộc D, dễ dàng nhận ra rất nhanh. Vậy xong, D là đáp án
Qua vài ví dụ trên chắc bạn nào chưa biết thì cũng đã hiểu cách chọn đáp án nhanh này. Dạng bài pp tọa độ không gian, việc ra đề mà bị học sinh thử đáp án là khó tránh khỏi. Nên các bạn cứ yên tâm học chắc "CƠ BẢN" là đủ đã có đất diễn cho các bạn chọn đáp án rồi! Lưu ý 1 lần nữa là các bạn ở nhà luyện theo chuyên đề thì cứ giải tay, đừng ỷ lại kiểu này, mà không nắm vững kiến thức cơ bản là vẫn khó chọn nhanh lắm.
