- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. Khoảng cách từ một điểm đến đường thẳng
Việc dựng hình chiếu của một điểm trên đường thẳng trong không gian, ta có thể làm theo
2 cách sau:
- Dựng mặt phẳng đi qua điểm và đường thẳng đã cho. Rồi trên mặt phẳng đó qua điểm
đã cho dựng đoạn vuông góc từ điểm tới đường thẳng.
- Dựng một mặt phẳng đi qua điểm đã cho và vuông góc với đường thẳng, lúc đó giao
điểm của đường thẳng với mặt phẳng vừa dựng chính là hình chiếu của điểm trên đường
thẳng.
Tính toán: Sau khi đã xác định được khoảng cách cần tính, ta dùng các hệ thức lượng
trong tam giác, đa giác, đường tròn, ... để tính toán.
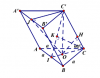
ví dụ 1: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều tâm O, cạnh a, hình
chiếu của C’ trên mp(ABC) trùng với tâm của đáy. Cạnh bên CC’ hợp với mp(ABC) góc
[tex]60^o[/tex] . Gọi I là trung điểm của AB. Tính khoảng cách từ O đến CC'.
theo giả thiết, CO' vuông (ABC), suy ra OC là hình chiếu của CC" lên (ABC).
suy ra[tex](CC',(ABC))=C'CO[/tex]
trong mặt phẳng (CC'O) dựng OH vuông CC' tại H.
ta có: [tex](O,CC')=OH[/tex]
xét tam giác vuông COH, suy ra [tex]OH=OC.sin30^o=\frac{a}{2}[/tex]
II. khoảng cách từ điểm đến mặt phẳng
với bài toán này, ta có thể xử lý bằng 2 cách:
- tìm hình chiếu vuống góc của điểm xuống mặt phẳng và tìm độ dài của đoạn thẳng đó.
- sử dụng công thức thể tích để suy ra khoảng cách của diểm đến mặt phẳng đáy.
III. khoảng cách từ đường thẳng đến mặt phẳng
Việc tính khoảng cách giữa một đường thẳng và một mặt phẳng song song với nó, hoặc
tính khoảng cách giữa hai mặt phẳng song song đều quy về việc tính khoảng cách từ điểm
đến mặt phẳng. Cần lưu ý việc chọn điểm trên đường hoặc trên mặt sao cho việc xác định
khoảng cách được đơn giản nhất.
IV. Khoảng cách giữa 2 đường thẳng chéo nhau
khoảng cách giữa 2 đường thẳng chéo nhau có thể được tính thông qua 2 cách sau:
- tìm đoạn vuông góc chung của 2 đường thẳng. độ dài đoạn vuông góc chung là khoảng cách giữa chúng.
- tìm mặt phẳng chứa đường thẳng này và song song với đường thẳng kia. quy về khoảng cách từ đường thẳng đến mặt phẳng.
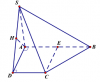
ví dụ 2: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, D, SA vuông góc với
đáy, [tex]SA=AD=a, AB=2a[/tex]. Tính khoảng cách giữa AB và SC.
Ta có: AB // DC nên
[tex]d(AB,SC)=d(AB,(SDC))[/tex].
từ A kẻ AH vuông góc SD, H nằm trong cạnh SD.
ta có: DC vuông AD và SA, nên DC vuông (SAD), do đó DC vuông AH.
suy ra AH vuông (SCD)
[tex]AH=d(AB,(SCD))=d(AB,SC)[/tex]
trong tam giác vuông SAD có:
[tex]\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{SA^2}=\frac{2}{a^2}=>AH=\frac{a}{\sqrt{2}}[/tex]
Việc dựng hình chiếu của một điểm trên đường thẳng trong không gian, ta có thể làm theo
2 cách sau:
- Dựng mặt phẳng đi qua điểm và đường thẳng đã cho. Rồi trên mặt phẳng đó qua điểm
đã cho dựng đoạn vuông góc từ điểm tới đường thẳng.
- Dựng một mặt phẳng đi qua điểm đã cho và vuông góc với đường thẳng, lúc đó giao
điểm của đường thẳng với mặt phẳng vừa dựng chính là hình chiếu của điểm trên đường
thẳng.
Tính toán: Sau khi đã xác định được khoảng cách cần tính, ta dùng các hệ thức lượng
trong tam giác, đa giác, đường tròn, ... để tính toán.
ví dụ 1: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều tâm O, cạnh a, hình
chiếu của C’ trên mp(ABC) trùng với tâm của đáy. Cạnh bên CC’ hợp với mp(ABC) góc
[tex]60^o[/tex] . Gọi I là trung điểm của AB. Tính khoảng cách từ O đến CC'.
theo giả thiết, CO' vuông (ABC), suy ra OC là hình chiếu của CC" lên (ABC).
suy ra[tex](CC',(ABC))=C'CO[/tex]
trong mặt phẳng (CC'O) dựng OH vuông CC' tại H.
ta có: [tex](O,CC')=OH[/tex]
xét tam giác vuông COH, suy ra [tex]OH=OC.sin30^o=\frac{a}{2}[/tex]
II. khoảng cách từ điểm đến mặt phẳng
với bài toán này, ta có thể xử lý bằng 2 cách:
- tìm hình chiếu vuống góc của điểm xuống mặt phẳng và tìm độ dài của đoạn thẳng đó.
- sử dụng công thức thể tích để suy ra khoảng cách của diểm đến mặt phẳng đáy.
III. khoảng cách từ đường thẳng đến mặt phẳng
Việc tính khoảng cách giữa một đường thẳng và một mặt phẳng song song với nó, hoặc
tính khoảng cách giữa hai mặt phẳng song song đều quy về việc tính khoảng cách từ điểm
đến mặt phẳng. Cần lưu ý việc chọn điểm trên đường hoặc trên mặt sao cho việc xác định
khoảng cách được đơn giản nhất.
IV. Khoảng cách giữa 2 đường thẳng chéo nhau
khoảng cách giữa 2 đường thẳng chéo nhau có thể được tính thông qua 2 cách sau:
- tìm đoạn vuông góc chung của 2 đường thẳng. độ dài đoạn vuông góc chung là khoảng cách giữa chúng.
- tìm mặt phẳng chứa đường thẳng này và song song với đường thẳng kia. quy về khoảng cách từ đường thẳng đến mặt phẳng.
ví dụ 2: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, D, SA vuông góc với
đáy, [tex]SA=AD=a, AB=2a[/tex]. Tính khoảng cách giữa AB và SC.
Ta có: AB // DC nên
[tex]d(AB,SC)=d(AB,(SDC))[/tex].
từ A kẻ AH vuông góc SD, H nằm trong cạnh SD.
ta có: DC vuông AD và SA, nên DC vuông (SAD), do đó DC vuông AH.
suy ra AH vuông (SCD)
[tex]AH=d(AB,(SCD))=d(AB,SC)[/tex]
trong tam giác vuông SAD có:
[tex]\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{SA^2}=\frac{2}{a^2}=>AH=\frac{a}{\sqrt{2}}[/tex]
