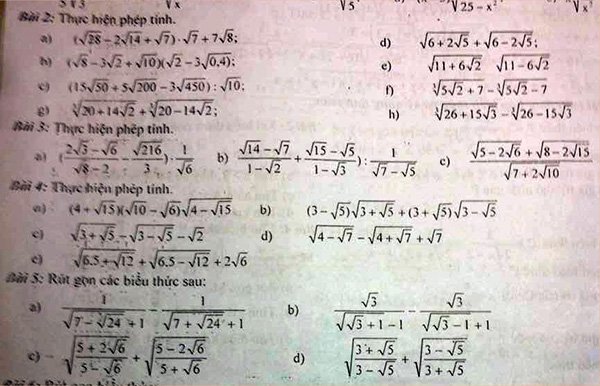2. Các câu a),b),c) là các câu biến đổi bình thường, em tự làm.
Câu d), e) có thể dùng cách phân tích biểu thức trong căn thành bình phương hoặc là đặt cả biểu thức là x, rồi tính [TEX]x^2[/TEX]
Câu f), g), h) đặt cả biểu thức là x, rồi tính [TEX]x^3[/TEX] với chú ý nếu [TEX]x=a+b[/TEX] thì [TEX]x^3=a^3+b^3+3ab(a+b)=a^3+b^3+3abx[/TEX]. (tương tự với [TEX]x=a-b[/TEX])
Tới đây giải phương trình ẩn x.
VD: f) Đặt [tex]x=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}> 0\Rightarrow x^3=5\sqrt{2}+7-(5\sqrt{2}-7)-3\sqrt[3]{(5\sqrt{2}-7)(5\sqrt{2}+7)}(\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7})=14-3x\Rightarrow x^3+3x-14=0\Rightarrow (x-2)(x^2+2x+7)=0\Rightarrow x=2[/tex]
3. Câu a), b) là câu biến đổi bình thường, em tự làm.
c) Gợi ý: [tex]\sqrt{5-2\sqrt{6}}=\sqrt{(\sqrt{3}-\sqrt{2})^2}=\sqrt{3}-\sqrt{2}[/tex], [tex]\sqrt{8-2\sqrt{15}}=\sqrt{(\sqrt{5}-\sqrt{3})^2}=\sqrt{5}-\sqrt{3}[/tex], [tex]\sqrt{7+2\sqrt{10}}=\sqrt{(\sqrt{5}+\sqrt{2})^2}=\sqrt{5}+\sqrt{2}[/tex]
4. a) Gợi ý: [tex](4+\sqrt{15})\sqrt{4-\sqrt{15}}=\sqrt{4+\sqrt{15}}.\sqrt{4+\sqrt{15}}.\sqrt{4-\sqrt{15}}=\sqrt{4+\sqrt{15}}.\sqrt{(4+\sqrt{15})(4-\sqrt{15})}=\sqrt{4+\sqrt{15}}=\sqrt{\frac{1}{2}(8+2\sqrt{15})}=\sqrt{\frac{1}{2}(\sqrt{5}+\sqrt{3})^2}=\frac{1}{\sqrt{2}}.(\sqrt{5}+\sqrt{3})[/tex]
b) Gợi ý: [tex]\sqrt{3+\sqrt{5}}=\sqrt{\frac{1}{2}(6+2\sqrt{5})}=\sqrt{\frac{1}{2}(\sqrt{5}+1)^2}=\frac{1}{\sqrt{2}}(\sqrt{5}+1)[/tex]
Tương tự với [TEX]\sqrt{3-\sqrt{5}}[/TEX]
Câu c),d),e) tách 2 căn đầu tiên rồi làm như câu f), g), h) của câu 2.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
