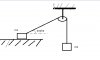
Xưa dạng bài này mình từng làm qua rồi, không dùng công cụ toán quá phức tạp.
Trước hết phải giải thích được vật rời bàn là do gì?
p/s: Đồng ý là N = 0 thì vật rời bàn, nhưng gì khiến N = 0?
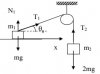
Các lực tác dụng lên m1 và m2 được biểu diễn
như hình vẽ.
Gọi a1, a2 là vận tốc và gia tốc của m1, m2 ở góc
lệch anpha bất kỳ khi m1 chưa rời bàn.
Áp dụng định luật II Niuton ta có:
Tcos(a)= ma1; Tsin(a)+ N1= mg; 2mg- T=m.a2
Tại thời điểm vật m1 bắt đầu rời khỏi mặt bàn: N1= 0
=> T=mg/sin(a) ; a1=g. cos(a) ; a2=g-g/2sin(a)................(0)
Do dây lí tưởng ta có:V1cos(a)=V2=> V1= V2/cos(a) .......... (1)
Đạo hàm hai vế:a1=a2/cos(a)+V2sin(a).a'/cos(a)^2 ..............(2)
x=H.cot(a) => V1= H.a'/sin(a)^2 ..........( H là k cach từ rr đến bàn ) ......(3)
từ (1) và (3) => a'=V2.sin(a)^2 / H.cos(a)...thay vào (2) =>
a1=v2^2.tan(a)^3/H+a2/cos(a) .....(4)
thay (0) vào (4) => (3+tan(a)^2) / 2tan(a)= 1/cos(a) + V2^2.tan(a)^3 / gH .......(5).
ĐLBTCN => ( m.V1^2+2m.V2^2)/2 = 2mg [tex]\Delta[/tex]h.........(6)
với [tex]\Delta h[/tex]= H/sin(30) - H/sin(a). thay vào(6) => V1^2+ 2V2^2=4gH
Từ (1) và (7): V2^2.(3+tan^2)=8gH(1-1/ 2sin(a)).....(8)
từ (5) và (8) =>[tex]\frac{3+tan(a)^{2}}{2.tan(a)}=\frac{1}{cos(a)}+\frac{8.tan(a)^{3}}{3+tan(a)^{2}}.(1-\frac{1}{2sin(a)})[/tex].
giải pt, đk a > 30 => a=45
( hình vẽ )
(em biết giải theo cách này thôi
. khi vật rời thì vật không còn chạm vào bàn nữa(0 tương tác với bàn ) nên N=0
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
