Giải hộ mình mấy bài nữa nha.
1,Cho a,b,c,d >0 và
Tìm max A=abcd
2,Tìm GTLN của B=
Bài 1:
Ta có: [tex]\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}+\frac{1}{1+d}\geq 3[/tex]
[tex]\rightarrow \frac{1}{1+a}\geq 1-\frac{1}{1+b}+1-\frac{1}{1+c}+1-\frac{1}{1+d}[/tex]
[tex]=\frac{b}{1+b}+\frac{c}{1+c}+\frac{d}{d+1}\geq 3\sqrt[3]{\frac{bcd}{(1+b)(1+c)(1+d)}}[/tex] (1) (áp dụng BĐT Cauchy)
Tương tự:
[tex]\frac{1}{1+b}\geq 3\sqrt[3]{\frac{acd}{(1+a)(1+c)(1+d)}}[/tex] (2)
[tex]\frac{1}{1+c}\geq 3\sqrt[3]{\frac{abd}{(1+a)(1+b)(1+d)}}[/tex] (3)
[tex]\frac{1}{1+d}\geq 3\sqrt[3]{\frac{bcd}{(1+b)(1+c)(1+d)}}[/tex] (4)
Nhân vế với vế các BĐT (1)(2)(3)(4) trên được:
[tex]\frac{1}{(1+a)(1+b)(1+c)(1+d)}\geq 3^{4}\sqrt[3]{\frac{a^{3}b^{3}c^{3}d^{3}}{(1+a)^{3}(1+b)^{3}(1+c)^{3}(1+d)^{3}}}=81.\frac{abcd}{(1+a)(1+b)(1+c)(1+d)}[/tex]
[tex]\Rightarrow abcd\leq \frac{1}{84}[/tex]
Dấu "=" xảy ra.................
Thôi tớ lười lắm rồi :v, chả muốn vt ra
[tex]a=b=c=d=\frac{1}{3}[/tex]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
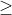 6.Hãy tìm GTNN của P=
6.Hãy tìm GTNN của P=



