(Ý tưởng lời giải: Phạm Gia Hưng - THPT Chuyên Võ Nguyên Giáp - Quảng Bình)
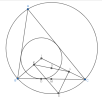
Gọi [imath]J, S,Q[/imath] lần lượt là tâm bàng tiếp góc [imath]A[/imath] và điểm chính giữa cung [imath]BC[/imath] lớn, nhỏ của [imath](O)[/imath]. [imath]U,V[/imath] lần lượt là chân đường vuông góc hạ từ [imath]S[/imath] lên [imath]BI, CI[/imath]. Gọi [imath]M, N, P[/imath] lần lượt là trung điểm [imath]BC, UV, KL[/imath].
Ta thấy [imath]\Delta ABD \sim \Delta AEC[/imath] nên [imath]AB \cdot AC=AE \cdot AD[/imath]
[imath]\Delta ABI \sim \Delta AJC \Rightarrow AB \cdot AC=AI \cdot AJ[/imath]
[imath]\Rightarrow AI \cdot AJ = AE \cdot AD \Rightarrow \Delta ADI \sim \Delta AJE \Rightarrow \widehat{ADI}=\widehat{AJE}[/imath]
(nếu như em học nghịch đảo đối xứng thì qua phép nghịch đảo đối xứng [imath]\mathcal{I}[/imath] có trục [imath]AI[/imath] và phương tích [imath]AB \cdot AC[/imath], [imath]I \leftrightarrow J[/imath] và [imath]D \leftrightarrow E[/imath] nên [imath]\widehat{ADI}=\widehat{AJE}[/imath])
Ta lại có [imath]=\widehat{AJE}=\widehat{ADI}=90^o-\widehat{ADB}=90^o-(\widehat{DAC}+\widehat{C})=90^o-\widehat{EAB}-\widehat{C}=\dfrac{1}{2}(\text{sđSQ-sđEB-sđAB})=\dfrac{1}{2}(\text{sđAS-sđEQ})[/imath] nên [imath]S,J,E[/imath] thẳng hàng.
Từ đó theo định lý Thales ta có [imath]\dfrac{KB}{KU}=\dfrac{EJ}{ES}=\dfrac{CL}{LV}[/imath]. Áp dụng bổ đề ERIQ ta có [imath]M,N,P[/imath] thẳng hàng.
Bây giờ ta chỉ cần chứng minh [imath]N[/imath] thuộc trung trực [imath]BC[/imath].
Lần lượt gọi [imath]I_a,I_b,I_c[/imath] là tâm đường tròn bàng tiếp góc [imath]A,B,C[/imath] của tam giác [imath]ABC[/imath].
Dễ thấy [imath](O)[/imath] là đường tròn Euler của tam giác [imath]I_aI_bI_c[/imath] nên [imath]S[/imath] là trung điểm của [imath]I_bI_c[/imath].
Từ đó [imath]SI_b=SI_c=SB[/imath] nên [imath]U[/imath] là trung điểm [imath]BI_b[/imath]. Từ đó [imath]UM[/imath] là đường trung bình tam giác [imath]BI_bC[/imath] nên [imath]UM \parallel CI_b[/imath] hay [imath]UM \perp CI[/imath].
Suy ra [imath]UM \parallel SV[/imath]. Tương tự [imath]SU \parallel VM[/imath] nên [imath]SUVM[/imath] là hình bình hành, suy ra [imath]S,N,M[/imath] thẳng hàng hay ta có điều phải chứng minh.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
