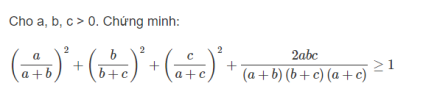Ta sẽ viết lại bài toán như sau:
Cho [imath]x,y,z[/imath] là các số thực dương thỏa mãn [imath]xyz=1[/imath]. Chứng minh rằng:
[math]\left (\dfrac{1}{x+1} \right )^2+ \left (\dfrac{1}{y+1} \right )^2+ \left (\dfrac{1}{z+1} \right )^2+\dfrac{2}{(x+1)(y+1)(z+1)}\geq 1[/math]Giải:
Theo nguyên lí Diriclet trong 3 số [imath]1-x,1-y,1-z[/imath] cùng dấu . Không mất tổng quát giả sử [imath](1-x)(1-y)\geq 0[/imath]
Ta có [math]\left (\dfrac{1}{x+1} \right )^2+ \left (\dfrac{1}{y+1} \right )^2+ \left (\dfrac{1}{z+1} \right )^2+\dfrac{2}{(x+1)(y+1)(z+1)}\geq \dfrac{1}{1+xy}+ \left (\dfrac{1}{z+1} \right )^2+\dfrac{2}{(x+1)(y+1)(z+1)}[/math]Ta sẽ chứng minh [math]\dfrac{1}{1+xy}+ \left (\dfrac{1}{z+1} \right )^2+\dfrac{2}{(x+1)(y+1)(z+1)}\geq 1[/math][math]\Leftrightarrow \dfrac{z}{1+z}+ \left (\dfrac{1}{z+1} \right )^2+\dfrac{2}{(x+1)(y+1)(z+1)} \ge 1[/math][math]\Leftrightarrow (z^2+z+1)(x+1)(y+1)+2(z+1)\geq (z+1)^2(x+1)(y+1)[/math][math]\Leftrightarrow 2(z+1)\geq z(x+1)(y+1)[/math][math]\Leftrightarrow z+xyz\geq z(x+y)[/math][math]\Leftrightarrow z+xyz\geq z(x+y)[/math][math]\Leftrightarrow 1+xy\geq x+y[/math][math]\Leftrightarrow (1-x)(1-y)\geq 0 (đúng)[/math]
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^
Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[Lý thuyết] Chuyên đề HSG : Bất đẳng thức
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
