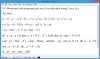
Câu 5 trước nhé ^^, cách của mình hơi dài nên có ai có cách hay hơn thì post lên nhé
Ta có HĐT: [TEX]x^3+y^3+z^3=(a+b+c)^3-3(a+b)(a+c)(b+c)[/TEX]
Áp dụng bđt Cô si, ta có:
[tex]2\sqrt{(a+b)(a+c)}\leq a+b+a+c=2a+b+c[/TEX]
Tương tự, ta có: [TEX]2\sqrt{(a+b)(b+c)}\leq a+2b+c[/TEX]
[TEX] 2\sqrt{(a+c)(b+c)}\leq a+b+2c[/tex]
Nhân các vế, ta đc:
[tex]8(a+b)(a+c)(b+c)\leq (a+2b+c)(a+b+2c)(2a+b+c)[/TEX]
[TEX]\Leftrightarrow -24(a+b)(a+c)(b+c)\geq -3(a+2b+c)(a+b+2c)(2a+b+c)[/TEX]
[TEX]\Leftrightarrow 8(a+b+c)^3-24(a+b)(a+c)(b+c)\geq 8(a+b+c)^3-3(a+2b+c)(a+b+2c)(2a+b+c)[/TEX]
[TEX]\Leftrightarrow 8((a+b+c)^3-3(a+b)(a+c)(b+c))\geq (a+b+a+c+b+c)^3-3(a+2b+c)(a+b+2c)(2a+b+c)[/TEX]
[TEX] \Leftrightarrow 8(a^3+b^3+c^3)\geq (a+b)^3+(a+c)^3+(b+c)^3[/tex] (đpcm)
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.