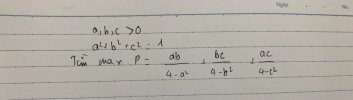Mọi người giúp em câu này với ạ, em cảm ơn ạ
Trung Ngo
Mọi người giúp em câu này với ạ, em cảm ơn ạ
[imath]P=\sum \dfrac{ab}{4-a^2}=\sum \dfrac{ab}{3+b^2+c^2} \leq \sum \dfrac{3ab}{8+2\sqrt{3}b+3c^2}[/imath]
Theo Cauchy-schwarz:
[imath]\sum \dfrac{3ab}{8+2\sqrt{3}b+3c^2} \leq \sum[\dfrac{2\sqrt{3}a}{121}+\dfrac{243ab}{121(8+3c^2)}][/imath]
mà [imath]a+b+c \leq \sqrt{3(a^2+b^2+c^2)}=\sqrt{3}[/imath]
nên [imath]\sum\dfrac{2\sqrt{3}a}{121} \leq \dfrac{6}{121}[/imath]
Bây h ta xét max của bthuc
[imath]M=\sum \dfrac{ab}{8+3c^2}=\sum \dfrac{ab}{5+3(1-a^2+1-b^2)} \leq \sum \dfrac{ab}{5+6\sqrt{(1-a^2)(1-b^2)}}[/imath]
Theo Cauchy-schwarz:
[imath]\sum \dfrac{ab}{5+6\sqrt{(1-a^2)(1-b^2)}}[/imath]
[imath]\leq \dfrac{5(ab+bc+ca)}{81} +\dfrac{4}{243}(\dfrac{b^2}{b^2+c^2}+\dfrac{c^2}{b^2+c^2}+\dfrac{a^2}{a^2+b^2}+\dfrac{b^2}{a^2+b^2}+\dfrac{a^2}{a^2+c^2}+\dfrac{c^2}{a^2+c^2})[/imath]
[imath]\leq \dfrac{5(a^2+b^2+c^2)}{81}+\dfrac{4}{81}=\dfrac{1}{9}[/imath]
Do đó,
[imath]p \leq \dfrac{6}{121}+\dfrac{1}{9}.\dfrac{243}{121}=\dfrac{3}{11}[/imath]
Dấu bằng xảy ra khi [imath]a=b=c=\dfrac{\sqrt{3}}{3}[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.