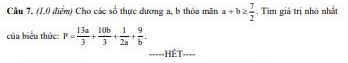Hướng giải:
Ta sẽ tách [imath]P=k(a+b)+(\dfrac{13}{3}-k)a+\dfrac{1}{2a}+(\dfrac{10}{3}-k)b+\dfrac{9}{b}[/imath]
[imath]\geq \dfrac{7}{2}k+2\sqrt{(\dfrac{13}{3}-k)\cdot \dfrac{1}{2}}+2\sqrt{(\dfrac{10}{3}-k)\cdot 9}[/imath]
Nhận thấy dấu "=" xảy ra khi [imath](\dfrac{13}{3}-k)a=\dfrac{1}{2a}, (\dfrac{10}{3}-k)b=\dfrac{9}{b},a+b=\dfrac{7}{2}[/imath]
[imath]\Leftrightarrow a=\sqrt{\dfrac{3}{2(13-3k)}},b=\sqrt{\dfrac{27}{10-3k}},a+b=\dfrac{7}{2}[/imath]
[imath]\Leftrightarrow \sqrt{\dfrac{3}{2(13-3k)}}+\sqrt{\dfrac{27}{10-3k}}=\dfrac{7}{2}[/imath]
Tới đây ta có thể ấn máy tính để tìm nghiệm [imath]k=\dfrac{7}{3}[/imath], hoặc ta đặt [imath]3k=t[/imath] rồi tìm [imath]t[/imath] sao cho từng cái căn đó là số hữu tỉ và thử lại là được.
Trình bày:
[imath]P=\dfrac{7}{3}(a+b)+2a+\dfrac{1}{2a}+b+\dfrac{9}{b} \geq \dfrac{7}{3} \cdot \dfrac{7}{2}+2\sqrt{2a \cdot \dfrac{1}{2a}}+2\sqrt{b \cdot \dfrac{9}{b}}[/imath]
[imath]=\dfrac{49}{6}+2+6=\dfrac{97}{6}[/imath]
Dấu "=" xảy ra tại [imath]x=\dfrac{1}{2}[/imath] và [imath]y=3[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
[Lý thuyết] Chuyên đề HSG : Bất đẳng thức
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
