[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
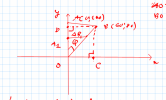
Hai con chuồn chuồn bay trên hai quỹ đạo khác nhau tại cùng một thời điểm. Một con bay trên quỹ đạo đường thẳng từ điểm A(0;100) đến điểm O(0,0) với vận tốc 5m/s . Con còn lại bay trên quỹ đạo đường thẳng từ từ điểm B(60;80) đến O(0;0) với vận tốc 10m/s . Hỏi trong quá trình bay, thì khoảng cách ngắn nhất mà hai con đạt được là bao nhiêu?