 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
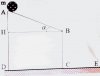
Từ điểm A của một mặt bàn phẳng nghiêng, người ta thả một vật có khối lượng m = 0,2kg trượt không ma sát với vận tốc ban đầu bằng 0 đến B rồi rơi xuống đất. Cho AB =1,3m; BC = 1m; AD = 1,3m,
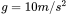 .
.
a, Vận tốc của vật tại điểm B và E có giá trị là?
b, Tìm khoảng cách giữa vị trí vật rơi với chân bàn CE.
c, Sau khi vật lún xuống đất một đoạn S bằng 2cm (dọc theo quỹ đạo). Tính lực cản trung bình của trái đất tác dụng lên vật.
Giúp mình nhé. Cảm ơn các bạn nhiều ạ.
@Death Game @Xuân Hiếu hust
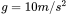
a, Vận tốc của vật tại điểm B và E có giá trị là?
b, Tìm khoảng cách giữa vị trí vật rơi với chân bàn CE.
c, Sau khi vật lún xuống đất một đoạn S bằng 2cm (dọc theo quỹ đạo). Tính lực cản trung bình của trái đất tác dụng lên vật.

Giúp mình nhé. Cảm ơn các bạn nhiều ạ.
@Death Game @Xuân Hiếu hust


