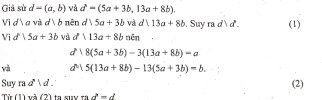Đề bài: hình bên dưới.
(a,b) kí hiệu của UCLN của a và b
Đáp án trong sách: Giải tương tự bài 5.
Bài 5: Chứng minh (a,b) = (5a+3b 13a+8b)
Đáp án bài 5: hình bên dưới.
(Cho phép mình dùng ảnh có đề bài luôn nha bởi vì viết kí hiệu khá lâu mà đề bài cũng dài nữa)
Dưa hấu mặt trờiCâu a mình xin phép sửa đề:
[imath]a) [a,b,c] = \dfrac{(a,b,c) .abc}{(a,b)(b,c)(c,a)}[/imath]
Có một cách chứng minh cũng khá hay, là bạn chứng minh dạng phân tích tiêu chuẩn của 2 vế giống nhau.
Nghĩa là với mọi số nguyên tố [imath]p[/imath] thì số mũ của chúng ở 2 vế là bằng nhau.
Gọi số mũ của số nguyên tố p trong phân tích tiêu chuẩn của [imath]a,b,c[/imath] lần lượt là [imath]x,y,z \in \mathbb{N}[/imath] .
Vì vai trò x,y,z như nhau, trực tiếp giả sử [imath]x\geq y \geq z[/imath]
Gọi tắt số mũ của p trong phân tích tiêu chuẩn của biểu thức A là [imath]v_p(A)[/imath]
****Các phép tính ở dưới sử dụng quy tắc lấy bcnn và ucln của các số theo phân tích tiêu chuẩn nhé.
Cụ thể BCNN thì lấy số mũ lớn nhất, UCLN lấy số mũ nhỏ nhất************
Khi này [imath]v_p(abc) = x+y+z ; v_p ( (a,b)) = x ; v_p( (b,c)) =y ; v_p ((c,a)) = x ; v_p((a,b,c)) =x[/imath]
[imath]\Rightarrow v_p (\dfrac{(a,b,c) .abc}{(a,b)(b,c)(c,a)} ) = x+y+z +x - x -y -x = z[/imath]
Lại có [imath]v_p( [a,b,c] ) = z[/imath]
Vậy suy ra [imath]v_p( [a,b,c] ) = v_p (\dfrac{(a,b,c) .abc}{(a,b)(b,c)(c,a)} )[/imath]
Như vậy bài toán được chứng minh
b) Câu này bạn sử dụng tính chất [imath]ab = [a,b]. (a,b)[/imath] là xong nhé, bạn thử xem !!
Ngoài ra bạn tham khảo thêm kiến thức tại : [Lý thuyết] Chuyên đề HSG: Số học [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.