[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
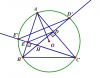
1. Cho tam giác ABC ( A<90 độ), nội tiếp đường tròn tâm O bán kính R vẽ các đường cao BD,CE, Các tia BD,CE lần lượt cắt (O) tại D',E'.
a) CMR: BEDC nội tiếp.
b) CMR: E'D'//ED.
c) CMR: OA vuông góc với ED.
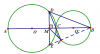
2.Cho 2 đường tròn tâm O và tâm O' tiếp xúc ngoài tại C, AC và BC là 2 đường kính của (O) và (O'). DE là dây cung của đường tròn tâm O vuông góc với AB tại trung điểm M của AB. Gọi giao điểm của đường thẳng DC và đường tròn tâm O' là F.
a)AEBD là hình gì?
b)CMR: B,E,F thẳng hàng.
c) CMR: MDBF nội tiếp.
a) CMR: BEDC nội tiếp.
b) CMR: E'D'//ED.
c) CMR: OA vuông góc với ED.
2.Cho 2 đường tròn tâm O và tâm O' tiếp xúc ngoài tại C, AC và BC là 2 đường kính của (O) và (O'). DE là dây cung của đường tròn tâm O vuông góc với AB tại trung điểm M của AB. Gọi giao điểm của đường thẳng DC và đường tròn tâm O' là F.
a)AEBD là hình gì?
b)CMR: B,E,F thẳng hàng.
c) CMR: MDBF nội tiếp.