Toán 9 Bài tập về điểm cố định

[Master Kaeton]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

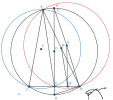
Cho đường tròn (O,R) và 2 điểm B,C phân biệt cố định trên đường tròn đó mà BC=a<2R. A bất kỳ trên cung lớn BC của (O) ( A không trùng với B,C ). AD là phân giác của tam giác ABC. E,F lần lượt là tâm đường tròn ngoại tiếp tam giác ADB và tam giác ADC.
Chứng minh khi A di chuyển trên đường tròn (O) thì E di chuyển trên 1 đường thẳng cố định.

Mong các bạn giúp mình bài này nhé. Mình cảm ơn nhìu <3
(Trước câu này có 2 câu là chứng minh tam giác AEO và tam giác ADC đồng dạng và tính diện tích tg AEOF theo a và R. Có thể có gợi ý từ 2 câu này á)

 

[TH trueMilk]

+ Đường trung trực của BC cắt cung lớn BC tại H, cắt cung nhỏ BC tại K. H, K là cố định
+ M, N là trung điểm của BD, AB [imath]\Rightarrow[/imath] góc BNE = góc BME = 90 độ
[imath]\Rightarrow[/imath] B, M, N, E cùng nằm trên đường tròn đường kính BE
[imath]\Rightarrow[/imath] [math]\overbrace{BME} = \overbrace{BNM} = \overbrace{BAD} = 1/4 sđ \overbrace{BKC}[/math]
[math]\overbrace{BKH} = 1/4 sđ\overbrace{BKC} \rightarrow \overbrace{BEM} = \overbrace{BHK} (1)[/math]Ta có EM song song HK. H, E cùng phía so với BC (2)
Kéo dài BE cắt HK tại H'. [math]\rightarrow \overbrace{BEM} = \overbrace{BH'K} (3)[/math]Từ 1, 2, 3 suy ra H trùng H' -> B, E, H thẳng hàng -> E thuộc BH cố định ( đpcm )