- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào mọi người 
Mình sẽ trình bày bài giải bên dưới và một số câu hỏi cho bài toán này nhé!
(Đề thi HSG lớp 9 tính Lào Cai 2020-2021)
Cho tam giác $ABC$ nhọn có $AB < AC$. Gọi $D$ là trung điểm của $BC$. Hai đường cao $BE$ và $CF$ cắt nhau tại $H$. Đường tròn tâm $O$ ngoại tiếp $\triangle{BDF}$ và đường tròn tâm $O'$ ngoại tiếp $\triangle{CDE}$ cắt nhau tại $I$ ($I$ khác $D$), $EF$ cắt $BC$ tại $K$. Chứng minh:
a) Tứ giác $AEIF$ nội tiếp
b) Tam giác $CDA$ đồng dạng với tam giác $DIC$
c) Ba đường thẳng $BE, CF, KI$ đồng quy
Lời giải.
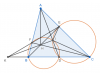
a) Những câu đầu tiên thường chỉ sử dụng đến biến đổi góc đơn giản. Thông qua các tứ giác nội tiếp $(O)$ và $(O')$ ta thu được các góc:
$$ \widehat{AEI} = \widehat{IDC} = \widehat{BFI} $$
Từ đó $AEIF$ là tứ giác nội tiếp.
b) Lỗi thường gặp: Do hình vẽ nhìn thấy ngay $A, I, D$ thẳng hàng nên đôi lúc các bạn sẽ quên chứng minh điều này, dẫn đến ngộ nhận và bị trừ điểm. Để chứng minh, các bạn cần sử dụng đến góc ở câu a như sau:
$$ \widehat{AIE} = \widehat{AFE} = \widehat{ACB} = 180^\circ - \widehat{DIE}$$
Từ đó $A, I, D$ thẳng hàng.
Tới đây $\triangle{DIC}$ và $\triangle{DCA}$ có chung đỉnh $D$, $\widehat{AIC} = \widehat{DEC} = \widehat{DCE}$ nên $\triangle{DIC} \sim \triangle{DCA}$
c) Đề nói vậy thôi, chứ mình nhận ra ngay là phải chứng minh $K, H, I$ thẳng hàng. Để chứng minh điều này thì ta quan sát:
Cách 1: $KH \perp AD$
Các bạn có thể làm một thao tác là: bỏ đi những gì không liên quan nữa. Ở đây, rõ ràng ta không còn liên quan gì đến $I$ nữa nên ta có thể quên nó đi trên hình vẽ hiện tại (hoặc bạn có thể vẽ một cái hình mới ngoài nháp như bên dưới)
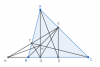
Khi đó, bạn sẽ thấy: để chứng minh bằng góc thì ta chỉ có thể chứng minh $\widehat{HKD} + \widehat{ADK} = 90^\circ$, và góc này dường như là hơi khó dùng, do $K$ và $H$ không có liên hệ gì chặt chẽ với nhau lắm.
Như vậy bạn có thể nghĩ theo cạnh: chứng minh dùng cạnh như thế nào nhỉ?
Ở đây bạn thấy, nếu ta chứng minh được $H$ là trực tâm thì ta sẽ được đpcm. Liệu có cách nào dùng cạnh để chứng minh không?
Câu trả lời là có: Gọi $G$ là giao của đường cao $AH$ với đáy thì ta chỉ cần chứng minh:
$$GK \cdot GD = GH \cdot GA$$
thì ta sẽ được $H$ là trực tâm (thông qua tam giác đồng dạng). Ta đi thêm một bước nữa để loại bỏ điểm $H$ ra khỏi đẳng thức:
$$GK \cdot GD = GB \cdot GC$$
do $H$ là trực tâm của $\triangle{ABC}$. Tới đây, bạn có thể tìm một đẳng thức khác liên quan đến $K, B, C, G, D$ để biến đổi về đẳng thức này, và đó là:
$$KB \cdot KC = KF \cdot KE = KG \cdot KD$$
Đây là phương tích của điểm $K$ đối với một số đường tròn. Bạn có thể tự làm tiếp nhé!...
Cách 2: $KI \perp AD$
Tương tự như trên, ta sẽ "quên đi" điểm $H$, đơn giản hóa hình vẽ:
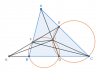
Ok, có một điều mình đồng ý là: cách 1 chưa được ổn lắm. Thực tế, cách trên khá là dài, và nó dựa vào rất nhiều thứ mà mình biết trước: đẳng thức về trực tâm, đẳng thức về phương tích, ... khiến nó không hề phù hợp với đề thi HSG này.
Để ý, mình sử dụng được ý đồ của câu a và câu b lắm. Tại sao lại chứng minh tam giác đồng dạng và điểm $I$ có vai trò gì?
Nếu bạn để ý, có vẻ như $KFIC$ là tứ giác nội tiếp?
$$\widehat{EFI} = \widehat{EAI} = \widehat{ICD}$$
Như vậy, nó nội tiếp thật. Từ đó $\widehat{KIC} = \widehat{KFC} = 90^\circ + \widehat{AFE}$
Mà $\widehat{KIC} = \widehat{KID} + \widehat{DIC}$ và $\widehat{AFE} = \widehat{DIC}$ nên suy ra $\widehat{KID} = 90^\circ$, đây là đpcm!
Câu hỏi
Mình sẽ trình bày bài giải bên dưới và một số câu hỏi cho bài toán này nhé!(Đề thi HSG lớp 9 tính Lào Cai 2020-2021)
Cho tam giác $ABC$ nhọn có $AB < AC$. Gọi $D$ là trung điểm của $BC$. Hai đường cao $BE$ và $CF$ cắt nhau tại $H$. Đường tròn tâm $O$ ngoại tiếp $\triangle{BDF}$ và đường tròn tâm $O'$ ngoại tiếp $\triangle{CDE}$ cắt nhau tại $I$ ($I$ khác $D$), $EF$ cắt $BC$ tại $K$. Chứng minh:
a) Tứ giác $AEIF$ nội tiếp
b) Tam giác $CDA$ đồng dạng với tam giác $DIC$
c) Ba đường thẳng $BE, CF, KI$ đồng quy
Lời giải.
a) Những câu đầu tiên thường chỉ sử dụng đến biến đổi góc đơn giản. Thông qua các tứ giác nội tiếp $(O)$ và $(O')$ ta thu được các góc:
$$ \widehat{AEI} = \widehat{IDC} = \widehat{BFI} $$
Từ đó $AEIF$ là tứ giác nội tiếp.
b) Lỗi thường gặp: Do hình vẽ nhìn thấy ngay $A, I, D$ thẳng hàng nên đôi lúc các bạn sẽ quên chứng minh điều này, dẫn đến ngộ nhận và bị trừ điểm. Để chứng minh, các bạn cần sử dụng đến góc ở câu a như sau:
$$ \widehat{AIE} = \widehat{AFE} = \widehat{ACB} = 180^\circ - \widehat{DIE}$$
Từ đó $A, I, D$ thẳng hàng.
Tới đây $\triangle{DIC}$ và $\triangle{DCA}$ có chung đỉnh $D$, $\widehat{AIC} = \widehat{DEC} = \widehat{DCE}$ nên $\triangle{DIC} \sim \triangle{DCA}$
c) Đề nói vậy thôi, chứ mình nhận ra ngay là phải chứng minh $K, H, I$ thẳng hàng. Để chứng minh điều này thì ta quan sát:
- $H$ hình như là trực tâm của $AKD$
- Ta có $\widehat{AIH} = 90^\circ$ do $AH$ là đường kính đường tròn đi qua $A,E,I,H,F$
- Nếu ta có $KH \perp AD$ hoặc $KI \perp AD$ nữa là ngon lành.
Cách 1: $KH \perp AD$
Các bạn có thể làm một thao tác là: bỏ đi những gì không liên quan nữa. Ở đây, rõ ràng ta không còn liên quan gì đến $I$ nữa nên ta có thể quên nó đi trên hình vẽ hiện tại (hoặc bạn có thể vẽ một cái hình mới ngoài nháp như bên dưới)
Khi đó, bạn sẽ thấy: để chứng minh bằng góc thì ta chỉ có thể chứng minh $\widehat{HKD} + \widehat{ADK} = 90^\circ$, và góc này dường như là hơi khó dùng, do $K$ và $H$ không có liên hệ gì chặt chẽ với nhau lắm.
Như vậy bạn có thể nghĩ theo cạnh: chứng minh dùng cạnh như thế nào nhỉ?
Ở đây bạn thấy, nếu ta chứng minh được $H$ là trực tâm thì ta sẽ được đpcm. Liệu có cách nào dùng cạnh để chứng minh không?
Câu trả lời là có: Gọi $G$ là giao của đường cao $AH$ với đáy thì ta chỉ cần chứng minh:
$$GK \cdot GD = GH \cdot GA$$
thì ta sẽ được $H$ là trực tâm (thông qua tam giác đồng dạng). Ta đi thêm một bước nữa để loại bỏ điểm $H$ ra khỏi đẳng thức:
$$GK \cdot GD = GB \cdot GC$$
do $H$ là trực tâm của $\triangle{ABC}$. Tới đây, bạn có thể tìm một đẳng thức khác liên quan đến $K, B, C, G, D$ để biến đổi về đẳng thức này, và đó là:
$$KB \cdot KC = KF \cdot KE = KG \cdot KD$$
Đây là phương tích của điểm $K$ đối với một số đường tròn. Bạn có thể tự làm tiếp nhé!...
Cách 2: $KI \perp AD$
Tương tự như trên, ta sẽ "quên đi" điểm $H$, đơn giản hóa hình vẽ:
Ok, có một điều mình đồng ý là: cách 1 chưa được ổn lắm. Thực tế, cách trên khá là dài, và nó dựa vào rất nhiều thứ mà mình biết trước: đẳng thức về trực tâm, đẳng thức về phương tích, ... khiến nó không hề phù hợp với đề thi HSG này.
Để ý, mình sử dụng được ý đồ của câu a và câu b lắm. Tại sao lại chứng minh tam giác đồng dạng và điểm $I$ có vai trò gì?
- Nếu đề yêu cầu mình chứng minh để sử dụng tính chất về cạnh, thì ta sẽ có:
$$DB^2 = DC^2 = DI \cdot DA$$
Và tới đây ta hy vọng $DB^2 = DG \cdot DK$ để suy ra $DI \cdot DA = DG \cdot DK$, nhưng nó sẽ lại dính tỉ lệ cạnh giữa $D, B, G, K$ và mình không muốn điều này. - Nói cách khác, ta cần dùng đến góc!
Nếu bạn để ý, có vẻ như $KFIC$ là tứ giác nội tiếp?
$$\widehat{EFI} = \widehat{EAI} = \widehat{ICD}$$
Như vậy, nó nội tiếp thật. Từ đó $\widehat{KIC} = \widehat{KFC} = 90^\circ + \widehat{AFE}$
Mà $\widehat{KIC} = \widehat{KID} + \widehat{DIC}$ và $\widehat{AFE} = \widehat{DIC}$ nên suy ra $\widehat{KID} = 90^\circ$, đây là đpcm!
Câu hỏi
- Hãy hoàn thiện lời giải ở cách 1 giúp mình nhé!
- Giả sử ta không dựng điểm $I$ như đề bài. Dựng $I$ là chân đường cao hạ từ $K$ xuống $AD$, bạn hãy chứng minh lại các tính chất:
- $D, H, I$ thẳng hàng
- $BFID$ và $CEID$ là các tứ giác nội tiếp