[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
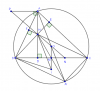
Cho tam giác ABC nhọn nội tiếp đường tròn (O), 3 đường cao AD, BE, CF giao nhau tại H. Đặt M là trung điểm BC, N đối xứng với D qua M. NH cắt đường thẳng song song BC qua A ở P. I đối xứng với O qua BC, A' đối xứng với H qua M.
a) CMR tứ giác ABA'C nội tiếp.
b) CMR [tex]\bigtriangleup APH \sim \bigtriangleup DNH; IH=IB[/tex]
Em xin cảm ơn!
a) CMR tứ giác ABA'C nội tiếp.
b) CMR [tex]\bigtriangleup APH \sim \bigtriangleup DNH; IH=IB[/tex]
Em xin cảm ơn!