[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 5: Tổng Hợp Hai Dao Động Điều Hòa Cùng Phương, Cùng Tần Số. Giản Đồ FRE-NEN
I. LÍ THUYẾT TRỌNG TÂM
1. Vectơ quay
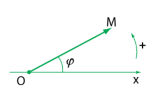
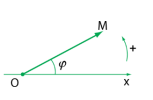
- Khi điểm [imath]M[/imath] chuyển động tròn đều thì vectơ vị trí [imath]OM[/imath] quay đều với cùng tốc độ góc [imath]\omega[/imath]. Khi ấy [imath]x = A\cos(\omega t + \varphi)[/imath] là phương trình hình chiếu của vectơ quay [imath]OM[/imath]― trên trục [imath]x[/imath].
- Biểu diễn phương trình của dao động điều hòa bằng một vectơ quay được vẽ tại thời điểm ban đầu như hình vẽ. Vectơ quay có những đặc điểm sau đây
|
2. Phương pháp giản đồ Fre-nen
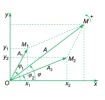
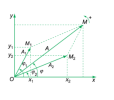
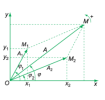
a) Tổng hợp hai dao động điều hòa cùng phương, cùng tần số- Tổng hợp hai dao động thành phần cùng phương : [imath]x_1 = A_1\cos(\omega t + \varphi_1)[/imath] và [imath]x_2 = A_2\cos(\omega t_2 + \varphi_2)[/imath] là chúng ta thực hiện phép tính [imath]x = x_1 + x_2[/imath] và kết quả ta thu được là một dao động tổng hợp x có dạng [imath]x = A\cos(\omega t + \varphi)[/imath]
|
+ Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó.
+ Biên độ và pha ban đầu của dao động tổng hợp được tính bằng các công thức sau đây: [imath]\begin{cases} A^2=A_1^2+A_2^2+2A_1A_2\cos\Delta \varphi \\ \tan \varphi = \dfrac{A_1\sin\varphi_1+A_2\sin\varphi_2}{A_1\cos\varphi_1+A_2\cos\varphi_2}\end{cases}[/imath]
3. Ảnh hưởng của độ lệch pha
Biên độ của dao động tổng hợp phụ thuộc vào các biên độ [imath]A_1, A_2[/imath] và độ lệch pha [imath](\varphi_2 - \varphi_1)[/imath] của các dao động thành phần.- Nếu các dao động thành phần cùng pha, tức [imath]\Delta \varphi = \varphi_2 - \varphi_1 = 2n\pi, (n = 0, \pm 1, \pm 2,...),[/imath] thì biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: [imath]A = A_1 + A_2.[/imath]
- Nếu hai dao động thành phần ngược pha, tức [imath]\Delta \varphi = \varphi_2 - \varphi_1 = (2n+1)\pi, (n = 0, \pm 1, \pm 2,...),[/imath] thì biên độ dao động tổng hợp là nhỏ nhất: [imath]A = |A_1 – A_2|.[/imath]
Câu hỏi sách giáo khoa
C1:
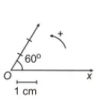
Biểu diễn dao động điều hòa [imath]x=3\cos\left(5t−\dfrac{\pi}{3}\right)cm[/imath] bằng một vectơ quay như hình vẽ.
|
C2:
| Ta có định lí hàm [imath]\cos[/imath] ta có: [math]\begin{aligned} &A^2=O M_1^2+M_1 M^2 2 O M_1 M_1 M . \cos \widehat{O M_1 M} \\ &\Leftrightarrow A^2=A_1^2+A_2{ }^2 2 A_1 A_2 \cos \left(\pi M_1 O M_2\right) \\ &\Leftrightarrow A^2=A_1^2+A_2^2+2 A_1 A_2 \cos \left(\pi+\widehat{M_1 O M_2}\right) \\ &\Leftrightarrow A^2=A_1^2+A_2{ }^2+2 A_1 A_2 \cos \left(\varphi_1 \varphi_2\right) \end{aligned}[/math] |
Chiếu [imath](1)[/imath] trục [imath]\mathrm{Ox}: \mathrm{A} \cos \varphi=\mathrm{A}_1 \cos \varphi_1+\mathrm{A}_2 \cos \varphi_2[/imath] (2)
Chiếu [imath](1)[/imath] trục [imath]\mathrm{Oy}: \mathrm{A} \sin \varphi=\mathrm{A}_1 \sin \varphi_1+\mathrm{A}_2 \sin \varphi_2[/imath] (3)
Lập tỉ số [imath](3) / (2)[/imath] ta được: [imath]\tan \varphi=\dfrac{A_1 \sin \varphi_1+A_2 \sin \varphi_2}{A_1 \cos \varphi_1+A_2 \cos \varphi_2}[/imath]
Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP