Bài tập SBT
[imath]1.1[/imath] Một chất điểm dao động điều hòa có quỹ đạo là một đoạn thẳng dài [imath]30cm[/imath]. Biên độ dao động của vật là
A. [imath]30cm[/imath]
B.[imath]15 cm[/imath]
C. [imath]-15 cm[/imath]
D. [imath]7,5 cm[/imath]
Lời giải :
Chọn B
[imath]A=\dfrac {30} {2} =15 cm[/imath]
[imath]1.2.[/imath] Tốc độ một vật dao động điều hòa cực đại khi nào ?
A. Khi [imath]t = 0[/imath]
B. Khi [imath]t = \dfrac T 4[/imath]
C. Khi [imath]t = \dfrac T 2[/imath]
D. Khi vật đi qua vị trí cân bằng
Lời giải :
Chọn D
Lí thuyết: Tốc độ một vật dao động điều hòa cực đại khi vật đi qua vị trí cân bằng
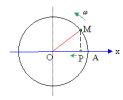
[imath]1.3.[/imath] Một điểm chuyển động tròn đều với tốc độ dài [imath]0,60 m/s[/imath] trên một đường tròn đường kính [imath]0,40 m[/imath]. Hình chiếu của nó lên một đường kính dao động điều hòa với biên độ, chu kì và tần số góc là:
A. [imath]0,40 m; 2,1 s ; 3,0 rad/s[/imath]
B. [imath]0,20 m; 0,48 s ; 3,0 rad/s[/imath]
C. [imath]0,20 m; 4,2 s ; 1,5 rad/s[/imath]
D. [imath]0,20 m; 2,1 s ; 3,0 rad/s[/imath]
Lời giải :
Chọn D
[imath]A=\dfrac {0,4}{2}=0,2(m)=r[/imath]
Ta có: [imath]v=r\omega \rightarrow 0,6=0,2 \omega \rightarrow \omega=3 rad/s[/imath]
[imath]T=\dfrac {2\pi}{\omega}=2,1s[/imath]
[imath]1.4.[/imath] Một vật dao động điều hòa theo phương trình [imath]x = 5\cos\pi t(cm)[/imath] . Tốc độ của vật có giá trị cực đại là
A. [imath]-5\pi(cm/s)[/imath].
B. [imath]5\pi(cm/s)[/imath].
C. [imath]5(cm/s)[/imath].
D. [imath]\dfrac 5 \pi(cm/s)[/imath].
Lời giải :
Chọn B
[imath]v_{max}=w.A=5\pi cm/s[/imath]
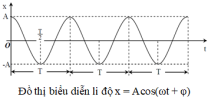
[imath]1.5.[/imath] Phương trình dao động điều hoà của một chất điểm là [imath]x = A\cos\left(\omega t - \dfrac \pi 2\right)cm[/imath]. Gốc thời gian được chọn vào lúc nào dưới đây?
A. Lúc chất điểm qua vị trí cân bằng theo chiều dương.
B. Lúc chất điểm qua vị trí cân bằng theo chiều âm.
C. Lúc chất điểm ở vị trí biên [imath]x = +A[/imath].
D. Lúc chất điểm ở vị trí biên [imath]x= -A[/imath].
Lời giải :
Chọn A
[imath]1.6.[/imath] Một vật nhỏ dao động điều hoà theo phương trình [imath]x = 10\cos\left(\pi t + \pi/6\right)(cm)[/imath]
Lấy [imath]\pi^2 = 10[/imath]. Gia tốc của vật có độ lớn cực đại là
A. [imath]10\pi cm/s^2[/imath].
B. [imath]10 cm/s^2[/imath].
C. [imath]100 cm/s^2[/imath].
D. [imath]100\pi cm/s^2[/imath].
Lời giải :
Chọn C
Gia tốc của vật có độ lớn cực đại là: [imath]a_{\max}=\omega^2.A=\pi^2.10=100 cm/s^2[/imath]
[imath]1.7.[/imath] Một chất điểm dao động điều hoà theo phương trình : [imath]x = 2\cos\left(2\pi t + \dfrac \pi 2\right)cm[/imath]. Tại [imath]t = 0,25 s[/imath] chất điểm có li độ bằng
A. [imath]\sqrt 3 cm[/imath].
B. [imath]-\sqrt 3 cm[/imath].
C. [imath]2[/imath] cm.
D. [imath]-2[/imath] cm.
Lời giải :
Chọn D
Thay [imath]t=0,25[/imath] vào phương trình li độ ta được [imath]x_t=-2cm[/imath]
[imath]1.8.[/imath] Một chất điểm dao động điều hoà trên trục [imath]Ox[/imath]. Khi chất điểm qua vị trí cân bằng thì tốc độ của nó là [imath]20 cm/s[/imath]. Khi chất điểm có tốc độ là [imath]10 cm/s[/imath] thì gia tốc của nó có độ lớn là [imath]40\sqrt 3 cm/s^2[/imath]. Biên độ dao động của chất điểm là
A. [imath]4cm.[/imath]
B. [imath]5 cm.[/imath]
C. [imath]8 cm.[/imath]
D. [imath]10cm.[/imath]
Lời giải :
Chọn B
Ta có: [imath]\dfrac{a^2}{a_{max}^2}+\dfrac{v^2}{v_{max}^2}=1[/imath]
[imath]\Rightarrow \dfrac {(40\sqrt 3)^2}{a_{max}^2}+ \dfrac{10^2}{20^2}=1[/imath]
[imath]\Rightarrow a_{max}=80 cm/s^2[/imath]
[imath]\Rightarrow A=\dfrac{v_{max}^2}{a_{max}}=5cm[/imath]
[imath]1.9.[/imath] Một chất điểm dao động điều hoà trên trục [imath]Ox[/imath]. Biết quãng đường đi được của chất điểm trong một chu kì dao động là [imath]16 cm[/imath]. Biên độ dao động của chất điểm bằng
A. [imath]16cm .[/imath]
B. [imath]4 cm[/imath].
C. [imath]32 cm[/imath].
D. [imath]8 cm[/imath].
Lời giải :
Chọn B
Trong [imath]1[/imath] chu kỳ chất điểm đi được quãng đường là [imath]4A=16cm\Rightarrow A=4cm[/imath]$
[imath]1.10.[/imath] Một chất điểm dao động điều hoà với chu kì [imath]1,25 s[/imath] và biên độ [imath]5 cm[/imath]. Tốc độ lớn nhất của chất điểm là
A. [imath]25,1 cm/s[/imath].
B. [imath]2,5 cm/s[/imath].
C. [imath]63,5 cm/s[/imath].
D. [imath]6,3 cm/s[/imath].
Lời giải :
Chọn A
Tốc độ lớn nhất của chất điểm là [imath]v_{max}=w.A=\dfrac{2\pi}{T}.5=\dfrac{2\pi}{1,25}.5=25,1327cm/s^2[/imath]
[imath]1.11.[/imath] Một chất điểm dao động điều hoà trên trục [imath]Ox[/imath]. Vectơ gia tốc của chất điểm có
A. độ lớn cực tiểu khi qua vị trí cân bằng, luôn cùng chiều với vectơ vận tốc.
B. độ lớn không đổi, chiều luôn hướng về vị trí cân bằng.
C. độ lớn cực đại ở vị trí biên, chiều luôn hướng ra biên.
D. độ lớn tỉ lệ với độ lớn của li độ, chiều luôn hướng về vị trí cân bằng.
Lời giải :
Chọn D
Lý thuyết SGK :Vecto gia tốc luôn hướng về vị trí cân bằng
[imath]1.12.[/imath] Một vật dao động điều hoà theo phương trình [imath]x = 0,05\cos10\pi t (m)[/imath]. Hãy xác định:
a) Biên độ, chu kì và tần số của vật.
b) Tốc độ cực đại và gia tốc cực đại của vật.
c) Pha của dao động và li độ của vật tại thời điểm [imath]t = 0,075 s[/imath].
a, Biên độ [imath]A=0,05m[/imath]
Chu kì [imath]T=\dfrac {2\pi}{w}=0,2s[/imath]
Tần số [imath]f=\dfrac 1 T=5 Hz[/imath]
[imath]1.13.[/imath] Một vật dao động điều hoà với biên độ [imath]A = 24 cm[/imath] và chu kì [imath]T = 4 s[/imath]. Tại thời điểm [imath]t = 0[/imath], vật có li độ là [imath]-A[/imath].
a) Viết phương trình dao động của vật.
b) Tính li độ, vận tốc và gia tốc của vật tại thời điểm [imath]t = 0,5 s[/imath].
c) Xác định thời điểm đầu tiên vật qua vị trí có li độ [imath]x = -12 cm[/imath] và tốc độ tại thời điểm đó.
Lời giải
a, Sử dụng vòng tròn lượng giác
[imath]\omega =\dfrac{2\pi}{T}=0,5\pi rad/s[/imath]
Phương trình dao động của vật là [imath]x=24\cos(0,5\pi t +\pi)[/imath]
b,Thay [imath]t[/imath] vào phương trình dao động ta được [imath]x_t=-16,9~17cm[/imath]
[imath]v_t=x'(t)=26,64 cm/s~27cm/s[/imath]
[imath]a_t=x''(t)=41,6cm/s^2=42cm/s[/imath]
c,Sử dụng trục thời gian
[imath]\Rightarrow[/imath] Vật từ biên âm đi theo chiều dương đến vị trí [imath]x=-12cm=-\dfrac A 2[/imath] hết [imath]\dfrac T {6} s=\dfrac 2 3 s[/imath]
[imath]v_t=x'(t)=32,6cm/s~33cm/s[/imath]
| [imath]1.14.[/imath] Xét một cơ chế truyền và biến đổi chuyển động (H.1.1). Hãy giải thích tại sao khi bánh xe quay đều thì pit-tông dao động điều hoà |  |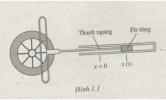
Lời giải
Xem thanh ngang là trục [imath]Ox[/imath] ,chuyển động của vòng tròn là [imath]1[/imath] chuyển động tròn đều có hình chiếu lên trục [imath]Ox[/imath] là [imath]1[/imath] dao động điều hoá từ đó làm pit tông dao động điều hoà
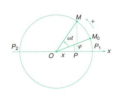
[imath]1.15.[/imath] Hai điểm [imath]M[/imath] và [imath]N[/imath] cùng chuyển động đều trên một đường tròn tâm [imath]O[/imath], bán kính, bán kính [imath]A[/imath], theo cùng một chiều và với cùng vân tốc góc [imath]\omega[/imath] (H.1.2). Hình chiếu [imath]P[/imath] của [imath]M[/imath] trên trục [imath]x[/imath] dao động theo phương trình [imath]x = A cos \omega t[/imath] và hình chiếu [imath]Q[/imath] của [imath]N[/imath]
trên trục [imath]Oy[/imath] dao động theo phương trình [imath]y = A \sin\left(\omega t + \dfrac \pi 2\right)[/imath]. Tính hiệu số pha dao động của chúng. |  |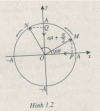
Lời giải
Vì [imath]\cos \omega t = \sin\left(\omega t + \dfrac{\pi}{2}\right)[/imath] nên 2 dao động cùng pha
[imath]\Rightarrow[/imath] Hiệu số pha bằng [imath]0[/imath]
Xem thêm:
[Vật lí 7] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 8] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 9] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 10] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 11] HỆ THỐNG MỤC MỤC CÁC LỚP
[Vật lí 12] HỆ THỐNG MỤC MỤC CÁC LỚP
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
