Nguyên tắc là: Viết pt dao động vật 1, pt dao động của vật 2 lệch so với vật 1 một góc a.
Xác định vị trí (theo phi) để khoảng cách là lớn nhất. Từ đó ta biết được mối quan hệ giữa góc phi và pha tại vị trí lớn nhất --> tính được khoảng cách hai vật theo pha đấy.
Cho khoảng cách bằng khoảng cách theo đề ---> tìm được độ lệch pha ban đầu phi.
Ta lập pt của vật 1 như sau: [TEX]x_1 = 3.cos(\omega.t)[/TEX], [TEX]x_2 = 6.cos(\omega.t + \varphi)[/TEX]
Tại vị trí khoảng cách cực đại, pha của 2 đang là x. Khoảng cách lúc này là:
[TEX]d_{max} = x_2 - x_1 = 6cos(x + \varphi) - 3cosx[/TEX]
Lấy đạo hàm của d theo x: [TEX]d' = 3sinx - 6sin(x+\varphi)[/TEX]. d cực đại khi d' = 0. Tức ta có pt: [TEX] 3sinx = 6sin(x+\varphi)[/TEX]
Về mặt ý nghĩa, pt d' = 0 có thể hiểu là khi đó vận tốc tương đối của 2 vật = 0, khi ấy khoảng cách giữa chúng là cực đại.
Mô tả pt trên lên đường tròn:
Pt [TEX]sinx = 2sin(x + \varphi)[/TEX] được thể hiện bằng 2 vecto như hình. (sin của vecto ngắn = sin của vecto dài).
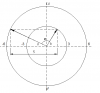
- Đặt góc bên trái là b, góc bên phải là a. Ta có hệ hai pt sau:
[TEX]6.sina = 3.sinb[/TEX]
[TEX]6.cosa + 3.cosb = 3\sqrt{3}[/TEX]
Phải giải hệ pt lượng giác trên để ra góc a, b, từ đó tính được độ lệch pha.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.



