2/ Khác với bạn trên, mình khuyên bạn nên vẽ các đoạn-khoảng ra các trục số khác nhau để dóng hàng cho dễ nhé. Lưu ý đầu tiên là: giao là lấy phần chung, còn hợp là lấy hết
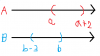
Để $A \cup B$ là một khoảng thì khi dóng hàng xuống, sẽ không tạo ra một khoảng trống nào ở giữa hết. Chẳng hạn như nếu đầu $b$ của $B$ thấp hơn đầu $a$ của $A$:
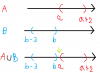
Như bạn thấy đó, nếu đầu $b$ thấp hơn đầu $a$ thì khi dóng xuống sẽ tạo ra một khoảng trống ở giữa, lúc này $A \cup B$ bị "hổng" ở giữa nên không thể là một khoảng được. Lúc này $A \cup B = (b-3;b) \cup (a;a+2)$ (giữa hai cái là một khoảng trống)
Như vậy thì đầu $b$ phải cao hơn đầu $a$, nhưng lỡ cao quá thì sao?
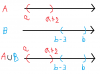
Lúc này nếu đầu $b$ lên cao quá thì lại kéo theo đầu $b-3$ cao theo, đến nỗi nó cao hơn đầu $a+2$ luôn nên vẫn tạo ra một khoảng trống ở giữa. Lúc này $A \cup B = (a;a+2) \cup (b-3;b)$ (giữa hai cái vẫn là khoảng trống)
Vậy cuối cùng ta cần cái gì?
- Đầu $b$ của $B$ cao hơn đầu $a$ của $A$, tạm viết là $b > a$
- Nhưng đừng cao quá, cao vừa vừa, đừng cho đầu $b-3$ cao hơn đầu $a+2$ là được, tạm viết lại là $b-3 < a+2$
- Dùng dấu bé hơn hay bé hơn hoặc bằng? Tùy trường hợp bạn nhé, nhưng do ở đây là hai ngoặc nhọn nên phải dùng dấu bé hơn thôi, hai đầu bằng nhau tức vừa "chạm" nhau thì vẫn bị hổng ở ngay điểm đó (bạn tưởng tượng nhé)
Vị trí như hình đầu tiên là bơ-phẹt, vì khi hợp lại thì $A \cup B = (b-2;a+2)$ đúng một khoảng luôn. Mình gửi lại cái hình
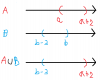
Ngoài ra còn một vị trí khác mà $A \cup B = (a;b)$ như thế này:
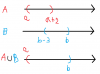
Tóm lại: Điều kiện bạn cần là $\begin{cases} b > a \\ b-2 < a+2 \end{cases}$ hay $-4 < a-b < 0$. Trình bày vậy thôi là đủ rồi, ngoài ra bạn có thể vẽ thêm một cái hình để minh họa cho đẹp
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
